已知二次函数的图象开口向上且不过原点0,顶点坐标为(1,-2),与x轴交于点A、B,与y轴交于点C,且满足关系式OC2=OA•OB.
(1)求二次函数的解析式;
(2)求△ABC的面积.
解:(1)∵抛物线顶点坐标为(1,-2),
设顶点式为y=a(x-1)
2-2=ax
2-2ax+a-2,A(x
1,0),B(x
2,0),
则x
1x
2=

,C(0,a-2),
由OC
2=OA•OB,得(a-2)
2=|x
1x
2|=|

|,即a
3-4a
2+4a=|a-2|,
当0<a<2时,有a
3-4a
2+5a-2=0
即(a-1)
2(a-2)=0,
解得a
1=1或a
2=2(舍去)
由a=1得y=x
2-2x-1;
当a>2时,有a
3-4a
2+3a+2=0
即(a-2)(a
2-2a-1)=0
解得a
1=2(舍去),a
2=1+

,a
3=1-

(舍去),
故a=1+

,y=(1+

)x
2-(2+2

)x+

-1,
故 所求二次函数解析式为:y=x
2-2x-1或y=(1+

)x
2-(2+2

)x+

-1;
(2)由S
△ABC=|AB|•|OC|,有两种情况:
①当y=x
2-2x-1时,
|AB|=|x
1-x
2|=

=2

,
又|OC|=1,故S
△ABC=

×2

×1=

;
②当y=(1+

)x
2-(2+2

)x+

-1时,
|AB|=|x
1-x
2|=

=2
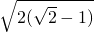
,
又|OC|=

-1,则
S
△ABC=

×2
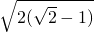
×(

-1)=(

-1)
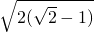
.
故所求△ABC的面积为(

-1)
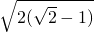
或

.
分析:(1)已知顶点坐标为(1,-2),可设顶点式为y=a(x-1)
2-2=ax
2-2ax+a-2,设A(x
1,0),B(x
2,0),则x
1x
2=

,C(0,a-2),由OC
2=OA•OB,将相应点的坐标代入,列方程求a,即可求二次函数解析式;
(2)根据二次函数解析式及AB=|x
1-x
2|,利用求根公式求AB,点C到线段AB的距离为高,可求△ABC的面积.
点评:本题考查了用待定系数法求二次函数解析式的方法.关键是根据条件确定抛物线解析式的形式,再求其中的待定系数.一般式:y=ax
2+bx+c(a≠0);顶点式y=a(x-h)
2+k,其中顶点坐标为(h,k);交点式y=a(x-x
1)(x-x
2),抛物线与x轴两交点为(x
1,0),(x
2,0).

 ,C(0,a-2),
,C(0,a-2), |,即a3-4a2+4a=|a-2|,
|,即a3-4a2+4a=|a-2|, ,a3=1-
,a3=1- (舍去),
(舍去), ,y=(1+
,y=(1+ )x2-(2+2
)x2-(2+2 )x+
)x+ -1,
-1, )x2-(2+2
)x2-(2+2 )x+
)x+ -1;
-1; =2
=2 ,
, ×2
×2 ×1=
×1= ;
; )x2-(2+2
)x2-(2+2 )x+
)x+ -1时,
-1时, =2
=2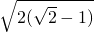 ,
, -1,则
-1,则 ×2
×2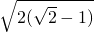 ×(
×( -1)=(
-1)=( -1)
-1)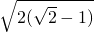 .
. -1)
-1)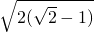 或
或 .
. ,C(0,a-2),由OC2=OA•OB,将相应点的坐标代入,列方程求a,即可求二次函数解析式;
,C(0,a-2),由OC2=OA•OB,将相应点的坐标代入,列方程求a,即可求二次函数解析式;

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案