练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．已知在平面直角坐标系中，点A、B、C、D的坐标依次为（-1，0），（m，n），（-1，10），（-9，p），且p≤n．若以A、B、C、D四个点为顶点的四边形是菱形，则n的值是4或5或18．

    分析 利用菱形的性质结合A，C点坐标进而得出符合题意的n的值．

    解答 解：如图所示：当C（-9，2），C′（-9，5）时，都可以得到以A、B、C、D四个点为顶点的四边形是菱形，
    同理可得：当D（-9，8）则对应点C的坐标为；（-9，18）可以得到以A、B、C、D四个点为顶点的四边形是菱形，
    故n的值为：4或5或18．
    故答案为：4或5或18．

    点评 此题主要考查了菱形的判定以及坐标与图形的性质，利用菱形的性质得出C点坐标是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．化简，再求值：（a-$\frac{2ab-{b}^{2}}{a}$）÷$\frac{a-b}{a}$，其中a=2，b=-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

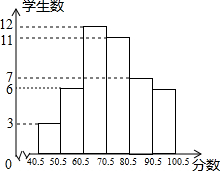    20．某班学生参加环保知识竞赛，已知竞赛得分都是整数．把参赛学生的成绩整理后分为6小组，画出竞赛成绩的频数分布直方图（如图所示），根据图中的信息，可得成绩高于60分的学生占全班参赛人数的百分率是80%．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．解不等式组：$\left\{\begin{array}{l}{5x-3＜4x，①}\\{4（x-1）+3≥2x，②}\end{array}\right.$ 请结合连意填空，完成本题的解答．
    （1）解不等式①，得x＜3；
    （2）解不等式②，得x≥$\frac{1}{2}$；
    （3）把不等式①和②的解集在数轴上表示出来：

    （4）原不等式组的解集为$\frac{1}{2}$≤x＜3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

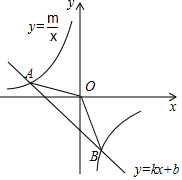    4．如图，已知A（-4，2）、B（a，-4）是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点；
    （1）求一次函数的解析式；
    （2）根据图象写出使一次函数的值小于反比例函数的值的x的取值范围；
    （3）求△AOB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．政府为解决老百姓看病难的问题，决定下调药品价格．某种药品经过两次降价后，每盒的价格由原来的60元降至48.6元，如果平均每次降价的百分率为x，则根据题意所列方程为60（1-x）2=48.6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．甲、乙、丙、丁四位同学一起研究一道数学题．如图，已知EF⊥AB，CD⊥AB，
    甲说：“如果还知道∠CDG=∠BFE，则能得到∠AGD=∠ACB．”
    乙说：“如果把甲的已知和结论倒过来，即由∠AGD=∠ACB，可得到∠CDG=∠BFE．”
    丙说：“∠AGD一定大于∠BFE．”
    丁说：“如果联结GF，则GF一定平行于AB．”
    他们四人中说法正确的有甲、乙．
    （填“甲”、“乙”、“丙”、“丁”）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，若∠CON=55°，则∠AOM的度数为（　　）
    A．35°B．45°C．55°D．65°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列运算不正确的是（　　）
    A．3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$B．a3+a4=a7C．a6÷a3=a3D．（3a3）2=9a6

    查看答案和解析>>

    同步练习册答案