
方程x2﹣x=0的解是( )
A. x=0 B. x=1 C. x1=0,x2=1 D. x1=0,x2=﹣1
C 【解析】试题分析:x2-x=0, x(x-1)=0, x=0或x-1=0, 所以x1=0,x2=1, 故选C.科目:初中数学 来源:安徽省豪州市心校2017-2018学年度第一学期期末八年级数学试卷 题型:填空题
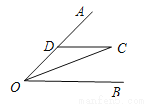
如图,已知OC平分∠AOB,CD∥OB,若OD=6㎝,则CD的长等于____________ .
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市蓬溪县2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
(2014•宁波)用矩形纸片折出直角的平分线,下列折法正确的是( )
A.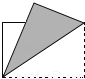 B.
B.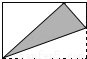 C.
C.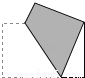 D.
D.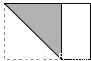
查看答案和解析>>
科目:初中数学 来源:山东省济南市历城区2018届九年级上学期期末考试数学试卷 题型:填空题
若一元二次方程x2﹣2x+a=0有两个相等的实数根,则a的值是_____.
1 【解析】∵一元二次方程x2﹣2x+a=0的二次项系数a=1,一次项系数b=﹣2,常数项c=a,且一元二次方程x2﹣2x+a=0有两个相等的实数根, ∴△=b2﹣4ac=0,即△=(﹣2)2﹣4×1×a=0, 解得a=1. 故答案是:1.查看答案和解析>>
科目:初中数学 来源:山东省济南市历城区2018届九年级上学期期末考试数学试卷 题型:单选题
在三角形纸片ABC中,AB=8,BC=4,AC=6.按下列四种方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )
A. 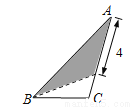 B.
B. 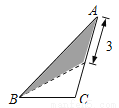
C. 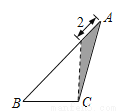 D.
D. 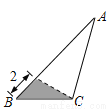
查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价七年级数学试卷 题型:解答题
如图,OD是∠AOB的平分线,OE是∠BOC的平分线,且∠AOC=130°,求∠DOE的度数.
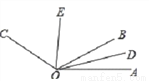
查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价七年级数学试卷 题型:填空题
某校图书室共藏书34500册,数34500用科学记数法表示为______.
3.45×104 【解析】试题解析:34500用科学记数法表示为 3.45×104, 故答案为:3.45×104.查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县2017-2018学年七年级上期末统一质量检测数学试卷 题型:解答题
星期日早晨,学校组织共青团员去参观雷锋纪念馆,小颖因故迟到没有赶上旅游车,于是她乘坐一辆出租车前往追赶,出租车司机说:“若以每小时80千米的速度,则需要1.5小时才能追上;若以每小时90千米的速度,则40分钟就能追上”.你知道出租车司机估计旅游车的速度是每小时多少千米吗?
出租车司机估计的旅游车速度是每小时72千米. 【解析】试题分析:设旅游车的速度是每小时千米,由“每小时行80千米,需1.5小时才能追上”,“每小时行90千米,40分钟就能追上”根据路程相等列出方程求解即可. 试题解析:设旅游车的速度是每小时千米,依题意得 , 解得. 答:出租车司机估计的旅游车速度是每小时72千米.查看答案和解析>>
科目:初中数学 来源:上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型:单选题
如图,△ABC在边长为1个单位的方格纸中,它的顶点在小正方形的顶点位置.如果△ABC的面积为10,且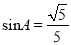 ,那么点C的位置可以在( )
,那么点C的位置可以在( )
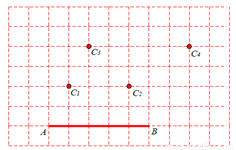
A. 点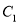 处 B. 点
处 B. 点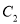 处 C. 点
处 C. 点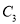 处 D. 点
处 D. 点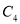 处
处
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com