
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
某电视机厂计划用两年的时间把某种型号的电视机的成本降低36%, 若每年下降的百分数相同,求这个百分数.
20% 【解析】本题主要考查了一元二次方程的应用. 可设原来的成本为1.等量关系为:原来的成本×(1-每年下降的百分数)2=原来的成本×(1-36%),把相关数值代入求合适解即可. 【解析】 设每年下降的百分数为x. 1×(1-x)2=1×(1-36%), ∵1-x>0, ∴1-x=0.8, ∴x=20%.查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:单选题
下面四个手机应用软件图标中是轴对称图形的是 ( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:填空题
甲、乙两台机床同时生产一种零件,在5天中,两台机床每天生产出的次品数分别如下表所列.
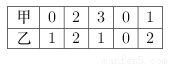
分析上述数据,请你估计这两台机床的性能_______比较稳定(填“甲”或“乙”或“无法确定”) .
乙 【解析】甲=(0+2+3+0+1)÷5=1.2, 乙=(1+2+1+0+2)÷5=1.2, S2甲= [(0-1.2)2+(2-1.2)2+(3-1.2)2+(0-1.2)2+(1-1.2)2]=1.36, S2乙= [(1-1.2)2+(2-1.2)2+(1-1.2)2+(0-1.2)2+(2-1.2)2]=0.56, S2甲>S2乙. 所以乙的性能比较稳...查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:单选题
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则弧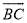 的长为( )
的长为( )
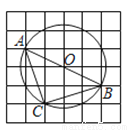
A. 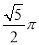 B.
B. 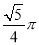 C.
C. 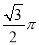 D.
D. 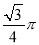
查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:解答题
将一批工业最新动态信息输入管理储存网络,甲独做需6小时,乙独做需4小时,甲先做30分钟,然后甲、乙一起做,则甲、乙一起做还需多少小时才能完成工作?
甲、乙一起做还需2小时12分才能完成工作 【解析】试题分析:30分=小时,可设甲、乙一起做还需x小时才能完成工作,等量关系为:甲小时的工作量+甲乙合作x小时的工作量=1,把相关数值代入求解即可. 【解析】 设甲、乙一起做还需x小时才能完成工作. 根据题意,得×+(+)x=1, 解这个方程,得x=, 小时=2小时12分, 答:甲、乙一起做还需2小时12分才能完成...查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:单选题
将一张宽为6的长方形纸片(足够长)折叠成如图所示图形.重叠部分是一个△ABC,则三角形ABC面积的最小值是( )
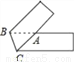
A. 9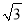 B. 18 C. 18
B. 18 C. 18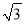 D. 36
D. 36
查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:解答题
已知一个长方形的周长为60cm.
(1)若它的长比宽多6cm,这个长方形的宽是多少cm?
(2)若它的长与宽的比是2:1,这个长方形的长是多少cm?
(1)这个长方形的宽是12cm;(2)这个长方形的长是20cm. 【解析】试题分析:(1)设长方形的宽为xcm,则长为(x+6)cm,根据长方形的周长为60cm列出方程解答即可; (2)设长方形的宽为acm,则长为2acm,根据长方形的周长为60cm列出方程解答即可. 试题解析:(1)设长方形的宽为xcm,则长为(x+6)cm,由题意得 2[x+(x+6)]=60, 解得...查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
如果一组数据a1,a2,…,an的方差是2,那么一组新数据2a1+1,2a2+1,…,2an+1的方差是( )
A. 2 B. 3 C. 4 D. 8
D 【解析】试题分析:∵一组数据a1,a2,…,an的方差是2,平均数为, ∴S2= [(a1-)2+(a2-)2+…+(an-)2]=2, ∵2a1+1,2a2+1,…,2an+1的平均数为2+1, ∴S′2= [(2a1+1-2-1)2+(2a2+1-2-1)2+…+(2an+1-2-1)2]=2×22=8, 故选D查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com