
如图,在Rt△ABC中,∠ACB=90°.
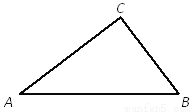
(1)利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
①作AC的垂直平分线,交AB于点O,交AC于点D;
②以O为圆心,OA为半径作圆,交OD的延长线于点E.
(2)在(1)所作的图形中,解答下列问题.
①点B与⊙O的位置关系是_;(直接写出答案)
②若DE=2,AC=8,求⊙O的半径.
(1)画图见解析;(2)(2)①点B在⊙O上;②⊙O的半径为5. 【解析】试题分析:(1)分别以A、C为圆心,以大于线段AC一半的长度在线段AC上下两侧画弧。连接交点级为线段AC的垂直平分线,交AB于点O,交AC于点D。 (2)比较OB和OA的长,如果OA=OB则点B 在圆上,利用垂直平分线的性质,及角与角之间的等量代换,可证明OA=OB。利用勾股定理,放在∆AOD中求半径。 试... 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源:浙江省杭州市白马湖2017-2018学年八年级上学期期中数学试卷(含解析) 题型:填空题
等腰三角形中有一个角等于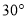 ,则这个等腰三角形的顶角度数是__________.
,则这个等腰三角形的顶角度数是__________.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型:解答题
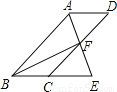
如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF平分∠ABE,EF=2,BF=4,求平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型:单选题
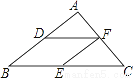
在△ABC中,AB=3,BC=4,AC=2,D,E,F分别为AB,BC,AC中点,连接DF,FE,则四边形DBEF的周长是( )
A. 5 B. 7 C. 9 D. 11
B 【解析】试题解析:∵D、E、F分别为AB、BC、AC中点, ∴DF=BC=2,DF∥BC,EF=AB=,EF∥AB, ∴四边形DBEF为平行四边形, ∴四边形DBEF的周长=2(DF+EF)=2×(2+)=7. 故选B.查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017届九年级上学期期末考试数学试卷 题型:解答题
已知:如图1,直线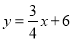 与x轴、y轴分别交于点A、C两点,点B的横坐标为2.
与x轴、y轴分别交于点A、C两点,点B的横坐标为2.
(1)求A、C两点的坐标和抛物线的函数关系式;
(2)点D是直线AC上方抛物线上任意一点,P为线段AC上一点,且S△PCD=2S△PAD ,求点P的坐标;
(3)如图2,另有一条直线y=-x与直线AC交于点M,N为线段OA上一点,∠AMN=∠AOM.点Q为x轴负半轴上一点,且点Q到直线MN和直线MO的距离相等,求点Q的坐标.
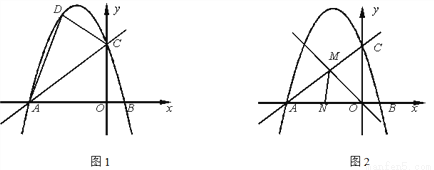
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017届九年级上学期期末考试数学试卷 题型:填空题
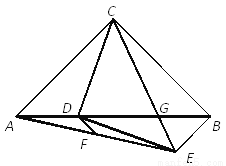
如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=8,BG=6,点F是AE的中点,连接DF,求线段DF的长_.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017届九年级上学期期末考试数学试卷 题型:填空题
据媒体报道,我国因环境污染造成的巨大经济损失,每年高达680000000元,这个数用科学记数法表示为______________元.
6.8×108 【解析】试题解析: 故答案为:查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型:解答题
先化简,再求值: 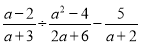 ,其中a=
,其中a=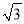 -2.
-2.
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
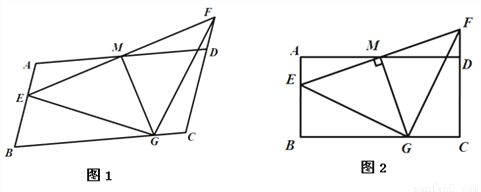
如图,在平行四边形ABCD中,AB=2,AD=4,M是AD的中点,点E是线段AB上一动点(可以运动到点A和点B),连接EM并延长交线段CD的延长线于点F.
(1) 如图1,①求证:AE=DF; ②若EM=3,∠FEA=45°,过点M作MG⊥EF交线段BC于点G,请直接写出△GEF的的形状,并求出点F到AB边的距离;
(2)改变平行四边形ABCD中∠B的度数,当∠B=90°时,可得到矩形ABCD(如图2),请判断△GEF的形状,并说明理由;
(3)在(2)的条件下,取MG中点P,连接EP,点P随着点E的运动而运动,当点E在线段AB上运动的过程中,请直接写出△EPG的面积S的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com