在直线y＝x+1上且位于x轴上方的所有点.它们的横坐标的取值范围是．题目和参考答案——青夏教育精英家教网—

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

科目：初中数学 来源： 题型：

如图，抛物线y＝a(x＋1)(x－5)与x轴的交点为M、N．直线y＝kx＋b

与x轴交于P(－2，0)，与y轴交于C．若A、B两点在直线y＝kx＋b上，且AO=BO=，AO⊥BO．D为线段MN的中点，OH为Rt△OPC斜边上的高．

1.OH的长度等于___________；k＝___________，b＝____________；

2.是否存在实数a，使得抛物线y＝a(x＋1)(x－5)上有一点E，满足以D、N、E为顶点的三角形与△AOB相似?若不存在，说明理由；若存在，求所有符合条件的抛物线的解析式，同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由)；并进一步探索对符合条件的每一个E点，直线NE与直线AB的交点G是否总满足PB·PG＜，写出探索过程．

查看答案和解析>>

科目：初中数学 来源：2012届浙江省杭州市春蕾、风帆、大成三校九年级第一次模拟数学卷（带解析） 题型：解答题

如图，抛物线y＝a(x＋1)(x－5)与x轴的交点为M、N．直线y＝kx＋b
与x轴交于P(－2，0)，与y轴交于C．若A、B两点在直线y＝kx＋b上，且AO=BO=，AO⊥BO．D为线段MN的中点，OH为Rt△OPC斜边上的高．
【小题1】OH的长度等于___________；k＝___________，b＝____________；
【小题2】是否存在实数a，使得抛物线y＝a(x＋1)(x－5)上有一点E，满足以D、N、E为顶点的三角形与△AOB相似?若不存在，说明理由；若存在，求所有符合条件的抛物线的解析式，同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由)；并进一步探索对符合条件的每一个E点，直线NE与直线AB的交点G是否总满足PB·PG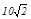＜，写出探索过程．

查看答案和解析>>

科目：初中数学 来源：2012年初中毕业升学考试（福建厦门卷）数学（解析版） 题型：解答题

如图，在平面直角坐标系中，已知点A(2，3)、B(6，3)，连结AB. 如果点P

在直线y＝x－1上，且点P到直线AB的距离小于1，那么称点P是线段AB的“邻近点”．

（1）判断点Ｃ(， ) 是否是线段AB的“邻近点”，并说明理由；

（2）若点Q (m，n)是线段AB的“邻近点”，求m的取值范围．

查看答案和解析>>

科目：初中数学 来源：2011-2012学年浙江省杭州市春蕾、风帆、大成三校九年级第一次模拟数学卷（解析版） 题型：解答题

如图，抛物线y＝a(x＋1)(x－5)与x轴的交点为M、N．直线y＝kx＋b

与x轴交于P(－2，0)，与y轴交于C．若A、B两点在直线y＝kx＋b上，且AO=BO=，AO⊥BO．D为线段MN的中点，OH为Rt△OPC斜边上的高．

1.OH的长度等于___________；k＝___________，b＝____________；

2.是否存在实数a，使得抛物线y＝a(x＋1)(x－5)上有一点E，满足以D、N、E为顶点的三角形与△AOB相似?若不存在，说明理由；若存在，求所有符合条件的抛物线的解析式，同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由)；并进一步探索对符合条件的每一个E点，直线NE与直线AB的交点G是否总满足PB·PG＜，写出探索过程．

查看答案和解析>>

练习册

高中

初中

小学