
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②③④ |
分析 利用抛物线的对称轴方程x=-$\frac{b}{2a}$<0可对①进行判断;抛物线与x轴最多有一个交点且抛物线开口向上,则y≥0,则可对②③进行判断;当x=-2时,y=4a-2b+c≥0,变形得到 a+b+c≥3(b-a),则利用b>a>0得到$\frac{a+b+c}{b-a}$≥3,则可对D进行判断.
解答 解:∵b>a>0,
∴抛物线的对称轴x=-$\frac{b}{2a}$<0,所以①正确;
∵抛物线与x轴最多有一个交点,
而抛物线开口向上,
∴关于x的方程ax2+bx+c=-2无实数根,所以②正确;
∵a>0及抛物线与x轴最多有一个交点,
∴x取任何值时,y≥0,
∴当x=-1时,a-b+c≥0;所以③正确;
当x=-2时,y=4a-2b+c≥0,
∴a+b+c≥3b-3a,
即a+b+c≥3(b-a),
而b>a>0,
∴$\frac{a+b+c}{b-a}$≥3,所以④正确.
故选D.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质.


科目:初中数学 来源: 题型:解答题
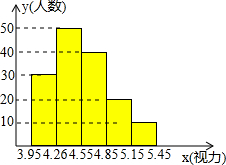 当今,青少年视力水平下降已引起了社会的关注,为了了解某校3000名学生的视力情况,从中抽取了一部分学生进行一次抽样调查,利用所得数据绘制的直方图(长方形的高表示该组人数)如图所示:
当今,青少年视力水平下降已引起了社会的关注,为了了解某校3000名学生的视力情况,从中抽取了一部分学生进行一次抽样调查,利用所得数据绘制的直方图(长方形的高表示该组人数)如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
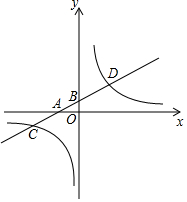 如图,在平面直角坐标系中,一次函数y1=kx+b的图象分别交x轴,y轴于A、B两点,与反比例函数y2=$\frac{n}{x}$的图象交于C、D两点,已知点C的坐标为(-4,-1),点D的横坐标为2.
如图,在平面直角坐标系中,一次函数y1=kx+b的图象分别交x轴,y轴于A、B两点,与反比例函数y2=$\frac{n}{x}$的图象交于C、D两点,已知点C的坐标为(-4,-1),点D的横坐标为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
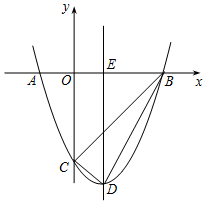 如图,抛物线y=x2+bx+c与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
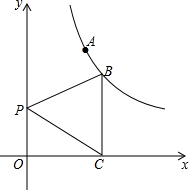 已知点A(1,2)、点 B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,
已知点A(1,2)、点 B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com