
如图,平面上有四个点A,B,C,D,请按要求画图:
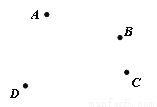
(1)作射线AB、DC交于点E;
(2)作线段AC,在线段AC上找到一点P,使其到B、D两个点的距离之和最短;
(3)作直线PE交线段AD于点M.
答案见解析. 【解析】试题分析:(1)根据射线的定义即可作出图形; (2)连接AC、BD交于点F,点F即为所求; (3)根据直线的定义即可作出图形. 试题解析:如图所示,科目:初中数学 来源:甘肃省2017-2018学年七年级上学期期中考试数学试卷 题型:填空题
已知|x+3|+(y﹣2)2=0,则xy=____.
9 【解析】∵,且, ∴,解得, ∴.查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级上学期第二次月考数学试卷 题型:单选题
下列方程为一元一次方程的是( )
A. 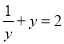 B.
B. 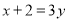 C.
C. 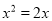 D.
D. 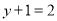
查看答案和解析>>
科目:初中数学 来源:山东省东营市2016-2017学年七年级上学期期中考试数学试卷 题型:单选题
已知∠α的补角为125°12′,则它的余角为( )
A. 35°12′ B. 35°48′ C. 55°12′ D. 55°48′
A 【解析】试题解析:∵∠α的补角为125°12′, ∴∠α=180°-125°12′=54°48′, ∴∠α的余角为: 90°-54°48′=35°12′. 故选A.查看答案和解析>>
科目:初中数学 来源:北京101中学2017-2018学年上学期初中七年级期末考试数学试卷 题型:解答题
阅读理【解析】
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离的2倍,我们就称点C是点是【A,B】的好点.
(1)如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点; 又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D 【A,B】的好点,点D 【B,A】的好点.(请在横线上填“是”或“不是”)
知识运用:
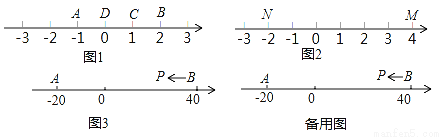
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2.数 所表示的点是【N,M】的好点;
(3)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.求当经过多少秒时,P、A和B中恰有一个点为其余两点的好点?
(1)不是,是(2)2或10(3)5秒或10秒或7.5秒. 【解析】试题分析:(1)根据定义发现:好点表示的数到【A,B】中,前面的点A是到后面的数B的距离的2倍,从而得出结论; (2)点M到点N的距离为6,分三等分为份为2,根据定义得:好点所表示的数为0或-8; (3)根据好点的定义可知分两种情况:①P为(A,B)的好点;②P为(B,A)的好点;③B为(A,P)的好点.设点P表...查看答案和解析>>
科目:初中数学 来源:北京101中学2017-2018学年上学期初中七年级期末考试数学试卷 题型:填空题
如图所示,O为直线AB上一点,OC平分∠AOE,∠DOE=90°,则以下结论正确的有____________.(只填序号)
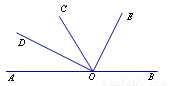
①∠AOD与∠BOE互为余角;
②OD平分∠COA;
③∠BOE=56°40′,则∠COE=61°40′;
④∠BOE=2∠COD.
①③④ 【解析】试题解析:∵∠DOE=90°, ∴∠COD+∠COE=90°,∠EOB+∠DOA=90°,(①正确) 若∠BOE=56°40′, ∵∠AOE+∠BOE=180°, ∴∠COE=(180°-∠BOE)=61°40′.(③正确) ∵OC平分∠AOE, ∴∠AOE=2∠COE=2∠AOC; ∵∠BOE=180°-2∠COE, ∴∠COD=90°-∠COE ∴∠...查看答案和解析>>
科目:初中数学 来源:北京101中学2017-2018学年上学期初中七年级期末考试数学试卷 题型:填空题
若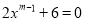 是关于x的一元一次方程,则m的值为_______.
是关于x的一元一次方程,则m的值为_______.
查看答案和解析>>
科目:初中数学 来源:陕西省西安市师大2017-2018学年初三期中考试数学试卷 题型:填空题
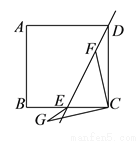
如图,四边形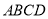 是边长为
是边长为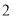 的正方形,
的正方形, 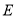 是
是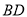 边的中点,
边的中点, 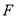 是直线
是直线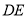 上的动点.连接
上的动点.连接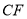 ,将线段
,将线段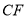 逆时针旋转
逆时针旋转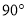 得到
得到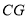 ,连接
,连接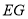 ,则
,则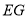 的最小值是__________.
的最小值是__________.
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:单选题
某人沿着倾斜角为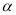 的斜坡前进了
的斜坡前进了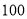 米,则他上升的高度是( ).
米,则他上升的高度是( ).
A. 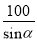 米 B.
米 B. 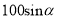 C.
C. 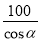 D.
D. 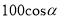 米
米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com