
 如图,正方形A1B1P1P2的顶点P1、P2在反比例函数
如图,正方形A1B1P1P2的顶点P1、P2在反比例函数 >0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数
>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数 >0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为________.
>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为________. +1,
+1, -1)
-1) ),则CP1=a,OC=
),则CP1=a,OC= ,易得Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D,则OB1=P1C=A1D=a,所以OA1=B1C=P2D=
,易得Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D,则OB1=P1C=A1D=a,所以OA1=B1C=P2D= -a,则P2的坐标为(
-a,则P2的坐标为( ,
, -a),然后把P2的坐标代入反比例函数y=
-a),然后把P2的坐标代入反比例函数y= ,得到a的方程,解方程求出a,得到P2的坐标;设P3的坐标为(b,
,得到a的方程,解方程求出a,得到P2的坐标;设P3的坐标为(b, ),易得Rt△P2P3F≌Rt△A2P3E,则P3E=P3F=DE=
),易得Rt△P2P3F≌Rt△A2P3E,则P3E=P3F=DE= ,通过OE=OD+DE=2+
,通过OE=OD+DE=2+ =b,这样得到关于b的方程,解方程求出b,得到P3的坐标.
=b,这样得到关于b的方程,解方程求出b,得到P3的坐标. 解:作P1C⊥y轴于C,P2D⊥x轴于D,P3E⊥x轴于E,P3F⊥P2D于F,如图,
解:作P1C⊥y轴于C,P2D⊥x轴于D,P3E⊥x轴于E,P3F⊥P2D于F,如图, ),则CP1=a,OC=
),则CP1=a,OC= ,
, -a,
-a, -a=
-a= ,
, ,
, -a),
-a), (x>0),得到(
(x>0),得到( -a)•
-a)• =2,解得a=-1(舍)或a=1,
=2,解得a=-1(舍)或a=1, ),
),
 =b,解得b=1-
=b,解得b=1- (舍),b=1+
(舍),b=1+ ,
, =
=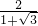 =
= -1,
-1, +1,
+1, -1).
-1). +1,
+1, -1).
-1).

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
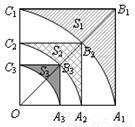
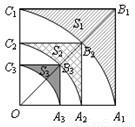
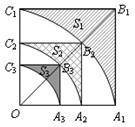 如图,正方形OA1B1C1的边长为2,以O为圆心、OA1为半径作弧A1C1交OB1于点B2,设弧A1C1与边A1B1、B1C1围成的阴影部分面积S1;然后以OB2为对角线作正方形OA2B2C2,又以O为圆心、OA2为半径作弧A2C2交OB2于点B3,设弧A2C2与边A2B2、B2C2围成的阴影部分面积为S2;…,按此规律继续作下去,设弧AnCn与边AnBn、BnCn围成的阴影部分面积为Sa.则S1=
如图,正方形OA1B1C1的边长为2,以O为圆心、OA1为半径作弧A1C1交OB1于点B2,设弧A1C1与边A1B1、B1C1围成的阴影部分面积S1;然后以OB2为对角线作正方形OA2B2C2,又以O为圆心、OA2为半径作弧A2C2交OB2于点B3,设弧A2C2与边A2B2、B2C2围成的阴影部分面积为S2;…,按此规律继续作下去,设弧AnCn与边AnBn、BnCn围成的阴影部分面积为Sa.则S1=查看答案和解析>>
科目:初中数学 来源:2011-2012学年辽宁省盘锦市四完中九年级(上)第四次月考数学试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2009-2010学年浙江省丽水市莲都区九年级(上)第三次月考数学试卷(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2010年北京市东城区中考数学二模试卷(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2010年浙江省杭州市萧山区中考数学模拟试卷47(河庄镇中 陈国亚)(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com