
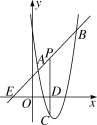
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( ,
, )和B(4,n),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,n),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:云南省楚雄州2017-2018学年七年级下学期期末教学质量监测数学试卷 题型:解答题
下列为边长为1的小正方形组成的网格图.
(1)请画出△ABC关于直线 对称的图形△A1B1C1(不要求写作法);
对称的图形△A1B1C1(不要求写作法);

(2)△ABC的面积为_____________(直接写出即可);
(3)如图,P为直线
 ,则点P到AC1的距离是_____________.
,则点P到AC1的距离是_____________.
查看答案和解析>>
科目:初中数学 来源:贵州省铜仁市2018年中考数学试卷 题型:单选题
掷一枚均匀的骰子,骰子的6个面上分别刻有1、2、3、4、5、6点,则点数为奇数的概率是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:安徽省毕业考试模拟冲刺数学卷(四) 题型:解答题
探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与 ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1,  ,2,
,2,  ,2
,2 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+(____) |
5×5 | (________) |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.

查看答案和解析>>
科目:初中数学 来源:安徽省毕业考试模拟冲刺数学卷(四) 题型:单选题
如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A20的坐标为 ( )
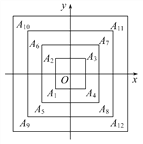
A. (5,5) B. (5,-5) C. (-5,5) D. (-5,-5)
查看答案和解析>>
科目:初中数学 来源:湖南省2018届九年级中考数学模拟试卷 题型:填空题
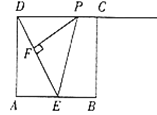
边长为2的正方形ABCD中E是AB的中点,P在射线DC上从D出发以每秒1个单位长度的速度运动,过P做PF⊥DE,当运动时间为__________秒时,以点P、F、E为顶点的三角形与△AED相似
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第二学期数学期中试卷 题型:单选题
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用



① ,②
,②


其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com