
 ,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.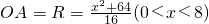 ;
;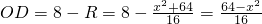 ,
,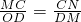 ,
,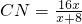 ;
;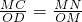 ,
,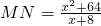 ;
;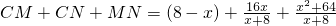 =(8-x)+(x+8)=16.
=(8-x)+(x+8)=16.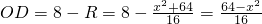 ,
,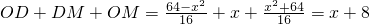 ;
;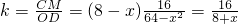 ;
;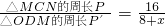 ,
,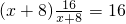 .
.

科目:初中数学 来源: 题型:
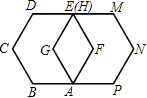 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )查看答案和解析>>
科目:初中数学 来源:初三数学圆及旋转题库 第8讲:弧长和扇形面积(解析版) 题型:解答题
 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com