练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：x＝3是关于x的方程3x－2a=1的解，则a的值是 ．

    4． 【解析】 试题分析：先把x=3代入得：9-2a=1，再解关于a的方程得：-2a=-8，即a=4．故答案为4．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年广东省东莞市堂星晨学校考数学模拟试卷 题型：解答题

    解不等式组： ．

    ﹣≤x＜1 【解析】试题分析：根据不等式的性质化简并计算每个不等式的取值范围，然后求两个范围的交集即可. 试题解析：解不等式2x＜，得：x＜1， 解不等式3（x+1）≥x+2，得：x≥﹣， 则不等式组的解集为﹣≤x＜1．

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版八年级数学下册（广西）期中测试 题型：单选题

    关于?ABCD的叙述，正确的是（　　）

    A. 若AB⊥BC，则?ABCD是菱形 B. 若AC⊥BD，则?ABCD是正方形

    C. 若AC=BD，则?ABCD是矩形 D. 若AB=AD，则?ABCD是正方形

    C 【解析】选项C中，满足矩形的判定定理：对角线相等的平行四边形是矩形，所以选C.

    查看答案和解析>>

    科目：初中数学 来源：青海省2017-2018学年七年级上学期12月月考数学试卷 题型：解答题

    某文艺团体为“希望工程”募捐组织了一场义演，共售出1000张票，筹出票款6920元，且每张成人票8元，学生票5元．

    （1）问成人票与学生票各售出多少张？

    （2）若票价不变，仍售出1000张票，所得的票款可能是7290元吗？为什么？

    （1）成人票640张，学生票360张；（2）不可能，理由见解析． 【解析】 试题分析：（1）设成人票x张，则学生票（1000－x）张，根据题意列出方程进行求解，得出答案；（2）设成人票y张，则学生票（1000－y）张，然后根据题意列出方程求出y的值，看y是否为整数，如果是整数则符合条件，如果不是整数则不符合条件． 试题解析：（1）设售出的成人票为x张，根据题意得：8x+5（100...

    查看答案和解析>>

    科目：初中数学 来源：青海省2017-2018学年七年级上学期12月月考数学试卷 题型：解答题

    计算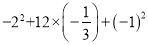

    -7 【解析】试题分析：按照有理数的混合运算顺序进行运算即可. 试题解析：原式

    查看答案和解析>>

    科目：初中数学 来源：青海省2017-2018学年七年级上学期12月月考数学试卷 题型：单选题

    某物品的标价为132元，若以9折出售，仍可获利10%，则该物品的进价是（　　　）

    A．118元 B.108元 C.106元 D. 104元

    B 【解析】 【解析】 设进价为x， 则依题意可列方程：132×90%x=10%•x， 解得：x=108元； 故选B．

    查看答案和解析>>

    科目：初中数学 来源：甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型：解答题

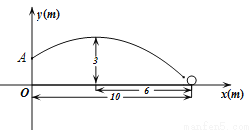
    如图，在某场足球比赛中，球员甲从球门底部中心点O的正前方10m处起脚射门，足球沿抛物线飞向球门中心线；当足球飞离地面高度为3m时达到最高点，此时足球飞行的水平距离为6m．已知球门的横梁高为2.44m．

    （1）在如图所示的平面直角坐标系中，问此飞行足球能否进球门？（不计其它情况）

    （2）守门员乙站在距离球门2m处，他跳起时手的最大摸高为2.52m，他能阻止球员甲的此次射门吗？如果不能，他至少后退多远才能阻止球员甲的射门？

    （1）能射中球门；（2）他至少后退0.4m，才能阻止球员甲的射门 【解析】试题分析：（1）根据条件可以得到抛物线的顶点坐标是（4，3），利用待定系数法即可求得函数的解析式； （2）求出当x=2时，抛物线的函数值，与2．52米进行比较即可判断，再利用y=2．52求出x的值即可得出答案． 试题解析：（1）抛物线的顶点坐标是（4，3）， 设抛物线的解析式是：y=a（x-4）2+3...

    查看答案和解析>>

    科目：初中数学 来源：甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型：单选题

    如图，已知AB是⊙O的直径，∠D=40°，则∠CAB的度数为( )

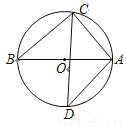
    A. 20° B. 40° C. 50° D. 70°

    C 【解析】∵∠D=40°， ∴∠B=∠D=40°. ∵AB是O的直径， ∴∠ACB=90°， ∴∠CAB=90°?40°=50°. 故选：C.

    查看答案和解析>>

    科目：初中数学 来源：2017年贵州省中考数学二模试卷 题型：解答题

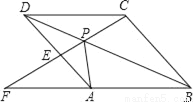
    如图，点P是菱形ABCD的对角线BD上一点，连结CP并延长，交AD于E，交BA的延长线于点F．

    试问：（1）图中△APD与哪个三角形全等？并说明理由．

    （2）求证：PA2=PE•PF．

    （1）（2）见解析 【解析】试题分析：（1）由菱形的性质可知： 又因为所以≌ （2）首先证明从而得到，故 试题解析：（1）≌ 理由：理由：∵四边形ABCD为菱形， ∴∠CDP=∠ADP，DC=AD. 在△APD和△CPD中, ∴≌ （2）∵≌ ∴∠DCP=∠DAP，PC=PA. ∵， ∴∠DCP=∠AFP. ∴∠DAP=∠AFP....

    查看答案和解析>>

    同步练习册答案