
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为( ,0)、(0,4),抛物线
,0)、(0,4),抛物线 经过B点,且顶点在直线
经过B点,且顶点在直线 上.
上.

(1)求抛物线对应的函数关系式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
(1)
(2)在,理由略
(3)M的坐标为( ,
, )
)
【解析】
解:(1)由题意,可设所求抛物线对应的函数关系式为 …(1分)
…(1分)
∴
∴ ……………………………………………………………(3分)
……………………………………………………………(3分)
∴所求函数关系式为: …………(4分)
…………(4分)
(2)在Rt△ABO中,OA=3,OB=4,
∴
∵四边形ABCD是菱形
∴BC=CD=DA=AB=5 ……………………………………(5分)
∴C、D两点的坐标分别是(5,4)、(2,0). …………(6分)
当 时,
时,
当 时,
时,
∴点C和点D在所求抛物线上. …………………………(7分)
(3)设直线CD对应的函数关系式为 ,则
,则

解得: .
.
∴ ………(9分)
………(9分)
∵MN∥y轴,M点的横坐标为t,
∴N点的横坐标也为t.
则 ,
,  ,……………………(10分)
,……………………(10分)
∴
∵ , ∴当
, ∴当 时,
时, ,
,
此时点M的坐标为( ,
, ). ………………………………(12分)
). ………………………………(12分)


科目:初中数学 来源: 题型:
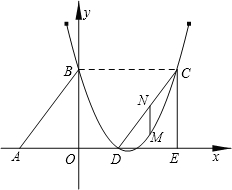 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=| 2 |
| 3 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
 象在第四象限的交点,AB⊥x轴于B,且S△ABO=
象在第四象限的交点,AB⊥x轴于B,且S△ABO=| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=| 2 |
| 3 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△ABO的顶点A是反比例函数y=
如图,Rt△ABO的顶点A是反比例函数y=| k |
| x |
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com