练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，已知C是线段AB上一点，AC∶BC＝1∶2，AB＝16 cm，D、E分别是线段AC、BC的中点，那么DE的长度是多少？若把AC∶BC的值改为2∶3，其他条件不变，那么DE的长度是多少？你能发现什么规律？用自己的语言描述出来．

    答案：
    解析：

    　　解：当AC∶BC＝1∶2时，根据题意，得

    　　DE＝AC＋BC＝AB＝×16＝8(cm)．

    　　当AC∶BC＝2∶3时，DE的长度仍为8 cm．

    　　规律：无论AC、BC的比值怎么变，DE的长度始终等于AB长度的一半．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，已知B是线段AE上一点，ABCD和BEFG都是正方形，连接AG、CE．
    （1）求证：AG=CE；
    （2）设CE与GF的交点为P，求证：
    PG
    CG
    =
    PE
    AG
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

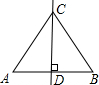    精英家教网如图，已知CD是线段AB的垂直平分线，垂足为D，E是CD上一点．若∠A=60°，则下列结论中错误的是（　　）
    A、AE=BEB、AD=BDC、AB=ACD、ED=AD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知C是线段AB的中点，则CD等于（　　）
    精英家教网
    A、AD-BD
    B、
    1
    2
    （AD-BD）
    C、
    1
    2
    AB-BD
    D、AD-
    1
    2
    AB

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•宿迁）如图，已知P是线段AB的黄金分割点，且PA＞PB，若S1表示PA为一边的正方形的面积，S2表示长是AB，宽是PB的矩形的面积，则S1
    =
    =
    S2．（填“＞”“=”或“＜”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）如图①，已知C是线段AB上一点，分别以AC、BC为边长在AB的同侧作等边△ADC与等边△CBE，试猜想AE与DB的大小关系，并证明．
    （2）如图②，当等边△CBE绕点C旋转后，上述结论是否仍成立？若成立，请证明；若不成立，请说明理由．

    查看答案和解析>>

    同步练习册答案