
�Ķ��⣺���ǰ��ܹ����ɷ�����ʽ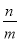 ��
��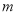 ��
��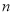 ��������
�������� 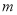 ������
������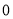 ����������������������ѭ��С��Ҳ������������������ô����
����������������������ѭ��С��Ҳ������������������ô����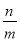 ��
��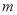 ��
��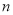 ��������
�������� 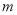 ������
������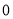 �����أ��뿴����ķ�����
�����أ��뿴����ķ�����
������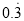 ������
������
��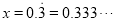 ��
��
��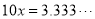 ��
��
���ɢ� �ڵã�
�ڵã� 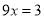 ����
����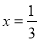 ��
�� 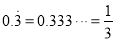
���ݲ��ϣ�������������
��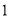 �����������ṩ�ķ�����
�����������ṩ�ķ�����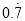 ��Ϊ��������
����������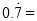 __________��
__________��
��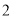 �����������ṩ�ķ�����
�����������ṩ�ķ�����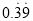 ��Ϊ������д�����̣�
��Ϊ������д�����̣�
 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡƽ���������2017-2018ѧ��ȵ�һѧ����ĩ��ѧ�Ծ����� ���ͣ������
һ���ִ���A��B����֮�亽�У�˳ˮ������Ҫ3Сʱ����ˮ������Ҫ5Сʱ����֪���ִ��ھ�ˮ�е��ٶ���12ǧ��ÿСʱ����A��B����֮��ľ��롣��������
��ˮ���ٶ�Ϊ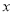 ǧ��ÿСʱ�����з���Ϊ�� ��
ǧ��ÿСʱ�����з���Ϊ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ������2017-2018ѧ����꼶��ѧ���ϣ���ĩģ���Ծ� ���ͣ���ѡ��
��һö�ʵؾ��ȵ�Ӳ��10�Σ�����˵����ȷ���ǣ�������
A. ����5�����泯�� B. ������5�����泯��
C. ��2�α���1�����泯�� D. ������10�����泯��
B ��������A.���DZ�Ȼ�¼�����B���� B.������¼�����C��ȷ�� C.���DZ�Ȼ�¼�����A���� D.������¼�����D���� ��ѡ��B.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2018��2017��������ĩ��̾� ���ͣ���ѡ��
����y=ax+1��y=ax2+bx+1��a��0����ͼ������ǣ�������
A. 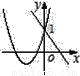 B.
B. 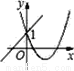 C.
C. 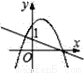 D.
D. 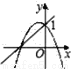
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2018��2017��������ĩ��̾� ���ͣ���ѡ��
�Ѻ���y=��2x2��ͼ������ƽ��1����λ��������ƽ��6����λ�����õ������ߵĺ�����ϵʽ�ǣ�������
A. y=��2��x��1��2+6 B. y=��2��x��1��2��6 C. y=��2��x+1��2+6 D. y=��2��x+1��2��6
C ��������ԭ�����ߵĶ�������Ϊ(1,3),����ƽ��2����λ,������ƽ��3����λ�õ��������ߵĶ�������Ϊ(?1,6).�����������ߵĽ���ʽΪ��y=?2(x?h) ²+k,����ã�y=?2(x+1) ²+6. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�꽭��ʡ�����г�һ��������ѧ�Ծ���ѧ�Ծ� ���ͣ������
����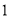 ��
��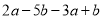 ����
����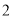 ��
��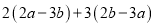 ��
��
��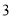 ��
��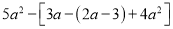 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�꽭��ʡ�����г�һ��������ѧ�Ծ���ѧ�Ծ� ���ͣ������
�����ϱ���������Ϊ������֮�Ρ���ɭ������ÿ�� ������ٶȴӵ�������ʧÿ��ɭ�ֵ���ʧ���ÿ�ѧ��������ʾӦΪ_____________���꣮
������ٶȴӵ�������ʧÿ��ɭ�ֵ���ʧ���ÿ�ѧ��������ʾӦΪ_____________���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ������Խ����2016-2017ѧ����꼶�²���ѧ��ĩ�����Ծ� ���ͣ������
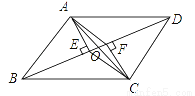
��ͼ��ƽ���ı���ABCD�У�AC��BD�ڵ�O��AE��BD��CF��BD������ֱ�ΪE��F����֤���ı���AECFΪƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�²ᣨ��ʦ��棩�����м���� ���ͣ������
ij��˾Ϊ������Ȥζ�˶�����ȡ�úóɼ���Ա�����ƻ�����ס������ֽ�Ʒ��20�������м��ֽ�Ʒÿ��40Ԫ�����ֽ�Ʒÿ��30Ԫ��
��1���������ס������ֽ�Ʒ��������650Ԫ����ס������ֽ�Ʒ�������˶��ټ���
��2������������ֽ�Ʒ�ļ������������ֽ�Ʒ������2�����ܻ��Ѳ�����680Ԫ����ù�˾���ļ��ֲ�ͬ�Ĺ�����
��1������ļס������ֽ�Ʒ�ֱ���5����15����2���ù�˾�����ֲ�ͬ�Ĺ���������һ��������ֽ�Ʒ7�����������ֽ�Ʒ13������������������ֽ�Ʒ8�����������ֽ�Ʒ12��. �������������������1�����ݡ����ֽ�Ʒ��20�����͡����ֽ�Ʒ������650Ԫ���г���������⼴�ɣ� ��2���������⣬�г�����ʽ����⼴��. �����������1����ס������ֽ�Ʒ�ֱ���x����y�� �����⣬�ã� ...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com