抛物线y=12-5x2的对称轴为轴.顶点坐标为．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

抛物线y=

-5x²的对称轴为______轴，顶点坐标为______．

抛物线y=

-5x²的对称轴为y轴，顶点为（0，

）．

练习册系列答案

赢在寒假期末闯关合肥工业大学出版社系列答案

快乐寒假山西教育出版社系列答案

创优教学中考必备中考试题精选系列答案

开心快乐假期作业寒假作业西安出版社系列答案

名题教辅寒假作业快乐衔接武汉出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

如图，⊙M与y轴的正半轴相切于点C，与x轴交于A（x₁，0）、B（x₂，0）两点，

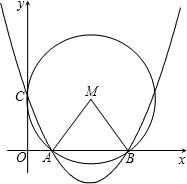且x₂＞x₁＞0，抛物线y=

（x²-5x+2m）经过A、B、C三点．
（1）求m的值；
（2）求sin∠AMB的值；
（3）在图中的曲线上是否存在点P，使以P、A、C为顶点的三角形与△COA相似？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

某水库管理处记录2010年水库的水位高度y（m）与月份x（月）之间的关系如图所示：在1月至6月份水位呈抛物线上升，到6月份达到最高水位，并且持续三个月，从9月份水位开始以直线下降，12月份水位达到最低．
（1）试写出2010年水库水位高度y（m）与月份x（月）之间的函数关系；
（2）当水位达到或超过9米时，水库水位处在警戒状态，试通过计算说明水库处在警戒时间为几个月？
（3）若该管理处利用水库资源，大力发展水上乐园，从1月份起每月游乐收入W（万元）与月份x（月）之间的函数关系式为W=

0.7x+10 (1≤x≤6)

-1.5x+23.2 (6＜x≤12)

，但水位到达警戒状态时，水上乐园必须关闭，暂停游乐．当警戒状态解除后，恢复游乐，问2010年该管理处游乐总收入为多少万元？
（4）为了在汛期水库和游客安全，并且在水位达到警戒状态时也能正常游乐，该管理处每月必须拿出资金进行防洪和维修，每月防洪维修费用Q（万元）与当月的水位高度y（m）之间的函数关系式为Q=

y，问2010年该管理处几月份的纯收入最高，最高为多少万元？（纯收入=游乐收入-防洪维修费用）

查看答案和解析>>

科目：初中数学 来源： 题型：

某水库管理处记录2011年水库的水位高度y（m）与月份x（月）之间的关系如图所示：在1月至6月份水位呈

抛物线上升，到6月份达到最高水位，并且持续三个月，从9月份水位开始以直线下降，12月份水位达到最低．
（1）试写出2011年水库水位高度y（m）与月份x（月）之间的函数关系；
（2）当水位达到或超过9米时，水库水位处在警戒状态，试通过计算说明水库处在警戒时间为几个月？
（3）若该管理处利用水库资源，大力发展水上乐园，从1月份起每月游乐收入W（万元）与月份x（月）之间的函数关系式为W=

0.7x+10(1≤x≤6)

-1.5x+23.2(6＜x≤12)

，但水位到达警戒状态时，水上乐园必须关闭，暂停游乐．当警戒状态解除后，恢复游乐，问2010年该管理处游乐总收入为多少万元？

查看答案和解析>>

科目：初中数学 来源： 题型：

（2011•包河区一模）蔬菜基地种植某种蔬菜，由市场行情分析可知，1月份到6月份这种蔬菜的市场售价p（元/千克）与上市时间x（月份）的关系为p=-1.5x+12，这种蔬菜每千克的种植成本y（元/千克）与上市时间x（月份）满足一个函数关系，这个函数的图象是抛物线一部分，如图所示．
（1）若图中抛物线经过A、B两点，对称轴是直线x=6，写出它对应的函数关系式；
（2）由以上信息分析，哪个月上市出售这种蔬菜每千克的收益最大？最大值是多少？
（收益=市场售价-种植成本）

查看答案和解析>>

科目：初中数学 来源： 题型：阅读理解

（2012•郴州）阅读下列材料：
我们知道，一次函数y=kx+b的图象是一条直线，而y=kx+b经过恒等变形可化为直线的另一种表达形式：Ax+Bx+C=0（A、B、C是常数，且A、B不同时为0）．如图1，点P（m，n）到直线l：Ax+By+C=0的距离（d）计算公式是：d=

|A×m+B×n+C|

A2+B2

．