
 如图,△AOD关于直线l进行轴对称变换后得到△BOC,下列说法中不正确的是
如图,△AOD关于直线l进行轴对称变换后得到△BOC,下列说法中不正确的是科目:初中数学 来源:2013年初中毕业升学考试(山东潍坊卷)数学(带解析) 题型:解答题
如图,抛物线 关于直线
关于直线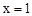 对称,与坐标轴交于A、B、C三点,且AB=4,点D
对称,与坐标轴交于A、B、C三点,且AB=4,点D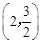 在抛物线上,直线
在抛物线上,直线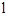 是一次函数
是一次函数 的图象,点O是坐标原点.
的图象,点O是坐标原点.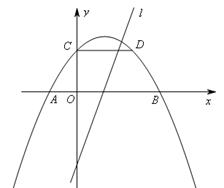
(1)求抛物线的解析式;
(2)若直线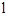 平分四边形OBDC的面积,求k的值.
平分四边形OBDC的面积,求k的值.
(3)把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线与直线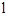 交于M、N两点,问在y轴正半轴上是否存在一定点P,使得不论k取何值,直线PM与PN总是关于y轴对称?若存在,求出P点坐标;若不存在,请说明理由.
交于M、N两点,问在y轴正半轴上是否存在一定点P,使得不论k取何值,直线PM与PN总是关于y轴对称?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.∠DAO=∠CBO,∠ADO=∠BCO |
| B.直线l垂直平分AB、CD |
| C.△AOD和△BOC均是等腰三角形 |
| D.AD=BC,OD=OC |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com