已知三角形的三边依次为n2-1,2n,n2+1,当n取2至10这9个自然数时,得到9个不同的三角形,其中具有最小内角的三角形的三边长依次为________.
99,20,101
分析:首先由三角形的三边依次为n
2-1,2n,n
2+1,根据勾股定理的逆定理可得:此三角形是直角三角形,然后分别求得n取2至10这9个自然数时,9个不同的三角形的最小角的正弦值,根据正弦函数的增减性问题,可得当n=10时是具有最小内角的三角形,继而求得其三边长.
解答:∵三角形的三边依次为n
2-1,2n,n
2+1,
又∵(n
2-1)
2=n
4-2n
2+1,(2n)
2=4n
2,(n
2+1)
2=n
4+2n
2+1,
∴(n
2-1)
2+(2n)
2=(n
2+1)
2,
∴此三角形是直角三角形,
当n=2,则n
2-1=3,2n=4,n
2+1=5,
则最小角的正弦为:

;
当n=3,则n
2-1=8,2n=6,n
2+1=10,
则最小角的正弦为:
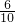
=

;
当n=4,则n
2-1=15,2n=8,n
2+1=17,
则最小角的正弦为:
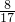
;
当n=5,则n
2-1=24,2n=10,n
2+1=25,
则最小角的正弦为:

=

;
当n=6,则n
2-1=35,2n=12,n
2+1=37,
则最小角的正弦为:

;
当n=7,则n
2-1=48,2n=14,n
2+1=50,
最小角的正弦为:

=

;
则当n=8,则n
2-1=63,2n=16,n
2+1=65,
则最小角的正弦为:

;
当n=9,则n
2-1=80,2n=18,n
2+1=82,
则最小角的正弦为:

=

;
∵

最小,即其对应的角最小,
当n=10,则n
2-1=99,2n=20,n
2+1=101,
则最小角的正弦为:
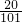
,
∵
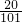
最小,即其对应的角最小,
∴当n
2-1=99,2n=20,n
2+1=101,
有最小内角,其三角形的三边长依次为99,20,101.
故答案为:99,20,101
点评:此题考查了三角形的边角关系,勾股定理的逆定理以及正弦函数的应用.此题难度较大,解题的关键是根据勾股定理的逆定理求得此三角形是直角三角形,然后根据正弦函数的性质求解,注意分类讨论思想的应用.

 ;
;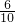 =
= ;
;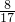 ;
; =
= ;
; ;
; =
= ;
; ;
; =
= ;
; 最小,即其对应的角最小,
最小,即其对应的角最小,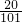 ,
,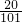 最小,即其对应的角最小,
最小,即其对应的角最小,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案