
 如图,A、B为两个新建生活小区,它们位于公路CD的同侧(沿公路CD已铺有宽带网).现要从公路CD上找一处接点,向A、B两个小区铺设宽带网.铺设工程费用为25000元/千米,已知AC=4km,BD=1km,CD=4km,则最少花费________元即可完成铺设工程.
如图,A、B为两个新建生活小区,它们位于公路CD的同侧(沿公路CD已铺有宽带网).现要从公路CD上找一处接点,向A、B两个小区铺设宽带网.铺设工程费用为25000元/千米,已知AC=4km,BD=1km,CD=4km,则最少花费________元即可完成铺设工程.
 解:作A点关于直线CD的对称点E,连接BE,与CD交于点P,则PA+PB最短,过E作EF∥CD与BD延长线交于点F,由作图可知,
解:作A点关于直线CD的对称点E,连接BE,与CD交于点P,则PA+PB最短,过E作EF∥CD与BD延长线交于点F,由作图可知, ,
, =25000
=25000 (元).
(元). .
.

科目:初中数学 来源: 题型:阅读理解
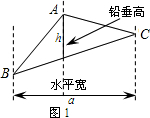
 阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 阅读材料:
阅读材料:| 1 | 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| |a| |
| a |
| |b| |
| b |
| |c| |
| c |
| |d| |
| d |
| |ab| |
| ab |
| |bc| |
| bc |
| |cd| |
| cd |
| |ad| |
| ad |

查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com