
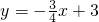 的图象与y轴、x轴相交于A、B,点C(m,n)在第二象限,⊙C与直线AB和x轴相切于E、F.
的图象与y轴、x轴相交于A、B,点C(m,n)在第二象限,⊙C与直线AB和x轴相切于E、F.
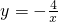 图象上时,求△CAB的面积.
图象上时,求△CAB的面积.
 (AB+OA+OB)=6,
(AB+OA+OB)=6, ,
, n,
n, n+n=
n+n= n,
n, =
= ,
, =
= ,
, =
= ,
,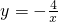 图象上时,
图象上时, ×AB×CF=
×AB×CF= ×5×2=5,
×5×2=5, x+3与x轴相交于点A,与y轴相交于点B,所以分别令x=0,y=0,可求出A(4,0),B(0,3),所以OA=4,OB=3,AB=5,连接CF,当四边形OBCE为矩形时,有CF=CE=OB=3,CB∥x轴,利用两直线平行同位角相等可得∠CBF=∠BAO,又因⊙C与直线AB相切于点F,所以CF⊥AB于点F,利用AAS可知△CBF≌△BAO,所以CB=AB=5,即点C的坐标为(-5,3);
x+3与x轴相交于点A,与y轴相交于点B,所以分别令x=0,y=0,可求出A(4,0),B(0,3),所以OA=4,OB=3,AB=5,连接CF,当四边形OBCE为矩形时,有CF=CE=OB=3,CB∥x轴,利用两直线平行同位角相等可得∠CBF=∠BAO,又因⊙C与直线AB相切于点F,所以CF⊥AB于点F,利用AAS可知△CBF≌△BAO,所以CB=AB=5,即点C的坐标为(-5,3); (AB+OA+OB)=6,又因由切线性质定理得,CE⊥x轴于点E,CD⊥y轴于点D,所以四边形CEOD为矩形,又因为CE=CD,所以四边形CEOD为正方形,所以OE=CE=r=AE-OA=6-4=2;
(AB+OA+OB)=6,又因由切线性质定理得,CE⊥x轴于点E,CD⊥y轴于点D,所以四边形CEOD为矩形,又因为CE=CD,所以四边形CEOD为正方形,所以OE=CE=r=AE-OA=6-4=2;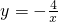 图象上时,所以可以求出m的值,即AB边上的高,利用三角形的面积公式即可求出△CAB的面积.
图象上时,所以可以求出m的值,即AB边上的高,利用三角形的面积公式即可求出△CAB的面积.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
 (2012•通州区一模)已知:如图,二次函数y=a(x+1)2-4的图象与x轴分别交于A、B两点,与y轴交于点D,点C是二次函数y=a(x+1)2-4的图象的顶点,CD=
(2012•通州区一模)已知:如图,二次函数y=a(x+1)2-4的图象与x轴分别交于A、B两点,与y轴交于点D,点C是二次函数y=a(x+1)2-4的图象的顶点,CD=| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
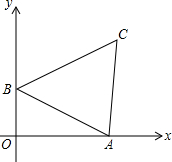 如图一次函数
如图一次函数 的图象与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等边三角形△ABC.
的图象与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等边三角形△ABC.查看答案和解析>>
科目:初中数学 来源:2004年江苏省苏州中学国际班、科少班招生考试数学试卷(解析版) 题型:解答题
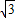 ,在BC边的延长线上取一点D,使CD=3.
,在BC边的延长线上取一点D,使CD=3.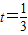 时,过点C作CH⊥PD于H,设K=7CH:9PD.求证:关于x的二次函数
时,过点C作CH⊥PD于H,设K=7CH:9PD.求证:关于x的二次函数 的图象与x轴的两个交点关于原点对称.
的图象与x轴的两个交点关于原点对称.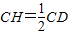 ?如果存在,请求出t的值;如果不存在,请说明理由.
?如果存在,请求出t的值;如果不存在,请说明理由.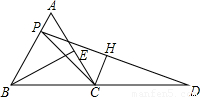
查看答案和解析>>
科目:初中数学 来源:2012年苏教版初中数学八年级下9.3反比例函数的应用练习卷(解析版) 题型:解答题
如图,一次函数的图象与x轴、y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,如果A点的坐标为(2,0),点C、D分别在第一、第三象限,且OA=OB= AC=BD,试求一次函数和反比例函数的解析式.
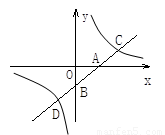
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com