
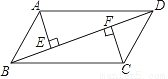
已知:如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ADE≌△CBF .
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源:内蒙古鄂尔多斯市2017-2018学年第一学期期中试卷初一数学. 题型:填空题
下表是围外城市与北京的时差(带正号的数表示同一时刻比北京时涧早的时数)如果现在是北京时间10:00,那么巴黎时间是____________.
城市 | 纽约 | 巴黎 | 东京 | 多伦多 |
时差(时) | -13 | -7 | +1 | -12 |
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷 题型:解答题
如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.
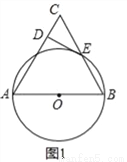
(1)试判断△ABC的形状,并说明理由;
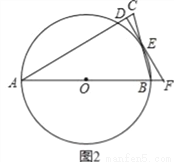
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=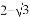 ,求⊙O的半径和BF的长
,求⊙O的半径和BF的长
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷 题型:单选题
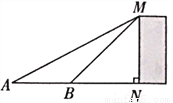
如图,为了测量某建筑物MN的高度,在平地上A处测得建筑物顶端M的仰角为30°,向N点方向前进16m到达B处,在B处测得建筑物顶端M的仰角为45°,则建筑物MN的高度等于( )
A. 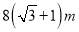 B.
B. 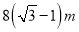 C.
C. 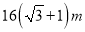 D.
D. 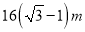
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷 题型:单选题
与﹣2的乘积为1的数是( )
A. 2 B. ﹣2 C.  D. ﹣
D. ﹣
查看答案和解析>>
科目:初中数学 来源:贵州省铜仁市松桃县2018届九年级上学期第二次月考数学试卷 题型:填空题
如图是一段楼梯,∠A=30°,斜边AC是4米,若在楼梯上铺地毯,则至少需要地毯______米.
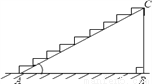
查看答案和解析>>
科目:初中数学 来源:贵州省铜仁市松桃县2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y= 的图象上,若菱形边长为4,则反比例函数解析式为( )
的图象上,若菱形边长为4,则反比例函数解析式为( )
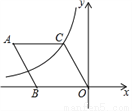
A. y=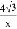 B. y=
B. y=
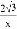 C. y=
C. y= 
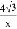 D. y=
D. y=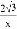
查看答案和解析>>
科目:初中数学 来源:山东省莒县第四协作区2017-2018学年度上学期第二次月考七年级数学试卷 题型:填空题
已知方程(a-2)x|a|-1+4=0是关于x的一元一次方程,那么a= .
-2 【解析】 试题分析:一元一次方程的定义:形如的方程就叫做一元一次方程. 由题意得,解得,则.查看答案和解析>>
科目:初中数学 来源:吉林省长春市2017-2018学年度 八年级数学期末测试卷 题型:单选题
-8的立方根为( )
A. 2 B. -2 C. ±2 D. ±4
B 【解析】试题解析: 的立方根是 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com