
如图,OC⊥AB,OD⊥OE,图中与∠1互余的角是__________.

科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
下面与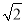 是同类二次根式的是( )
是同类二次根式的是( )
A. 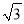 B.
B. 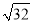 C.
C. 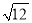 D.
D. 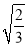
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
已知,CD是Rt △ABC斜边上的高,∠ACB=90o AC=4m,BC=3 m,则线段CD的长为 ( )
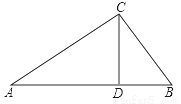
A. 5 m B. 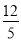 m C.
m C. 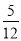 m D.
m D. 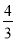 m
m
查看答案和解析>>
科目:初中数学 来源:辽宁省2017-2018学年八年级上学期期末模拟数学试卷 题型:单选题
如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,下列结论中不正确的是( )
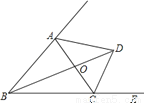
A. ∠BAC=70° B. ∠DOC=90° C. ∠BDC=35° D. ∠DAC=55°
B 【解析】试题分析:∵∠ABC=50°,∠ACB=60°,∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣50°﹣60°=70°,故A选项正确,∵BD平分∠ABC,∴∠ABO=∠ABC=×50°=25°,在△ABO中,∠AOB=180°﹣∠BAC﹣∠ABO=180°﹣70°﹣25°=85°,∴∠DOC=∠AOB=85°,故B选项错误; ∵CD平分∠ACE,∴∠ACD=(180°﹣...查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:解答题
如图,AD= DB,E是BC的中点,BE=
DB,E是BC的中点,BE=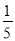 AC=2 cm,求线段DE的长.
AC=2 cm,求线段DE的长.

查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:填空题
一个正方体所有相对面上的两数之和相等,它的表面展开图如图所示,则x的值为_______.

查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:单选题
如果两个角互补,则( )
A. 这两个角都是锐角 B. 这两个角都是钝角
C. 这两个角一个是钝角一个是锐角 D. 以上说法都是不正确
D 【解析】因为互补的两个角的和等于180°,所以互补的两个角可能是一个锐角,一个钝角;或两个都是直角. 故选D.查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
下列线段不能构成直角三角形的是( )
A. a=6,b=8,c=10 B. a=1,b=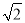 ,c=
,c=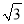
C. a=3,b=4,c=5 D. a=2,b=3,c=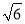
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
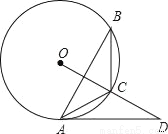
如图,△ABC内接于⊙O,过点A作⊙O的切线,交OC的延长线于点D,∠D=30°
(1)求∠B的度数;
(2)若OD⊥AB,BC=5,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com