
 如图,从点A(0,2)发出一束光,经x轴反射,过点B(4,3),则这束光从点A到点B所经过的路径的长为________.
如图,从点A(0,2)发出一束光,经x轴反射,过点B(4,3),则这束光从点A到点B所经过的路径的长为________.
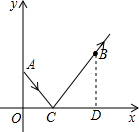 解:如图,过点B作BD⊥x轴于D,
解:如图,过点B作BD⊥x轴于D, OD=
OD= ×4=
×4= ,
,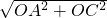 =
=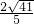 ,
,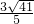 ,
, .
. .
. .
.

科目:初中数学 来源: 题型:
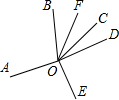 如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD的度数.
如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:
 (两题任选其一作答)
(两题任选其一作答)查看答案和解析>>
科目:初中数学 来源: 题型:
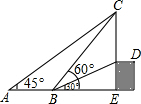 如图,从点A看一高台上的电线杆CD,顶端C的仰角为45°,向前走6米到B点,测得其顶端C和杆底D的仰角分别是60°和30°,求电线杆CD的高(精确到0.1米).
如图,从点A看一高台上的电线杆CD,顶端C的仰角为45°,向前走6米到B点,测得其顶端C和杆底D的仰角分别是60°和30°,求电线杆CD的高(精确到0.1米).查看答案和解析>>
科目:初中数学 来源: 题型:
 探照灯、锅形天线、汽车灯以及其他很多灯具都与抛物线形状有关.如图,从点O照射到抛物线上的光线OB,OC等反射以后沿着与POQ平行的方向射出.图中如果∠BOP=45°,∠QOC=88°,那么∠ABO和∠DCO各是多少度?
探照灯、锅形天线、汽车灯以及其他很多灯具都与抛物线形状有关.如图,从点O照射到抛物线上的光线OB,OC等反射以后沿着与POQ平行的方向射出.图中如果∠BOP=45°,∠QOC=88°,那么∠ABO和∠DCO各是多少度?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com