
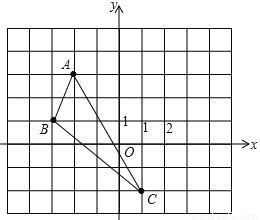
(1)画出△ABC关于y轴对称的图形△A1B1C1;
(2)在x轴上找出点P,使得点P到点A、点B的距离之和最短(保留作图痕迹)
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源:浙江杭州拱墅区锦绣育才2017-2018学年七年级上学期期中数学 题型:单选题
估计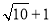 的值应在( ).
的值应在( ).
A. 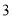 和
和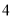 之间 B.
之间 B. 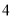 和
和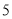 之间 C.
之间 C. 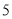 和
和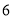 之间 D.
之间 D. 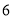 和
和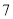 之间
之间
查看答案和解析>>
科目:初中数学 来源:吉林省吉林市2016-2017七年级数学上期期末试卷 题型:解答题
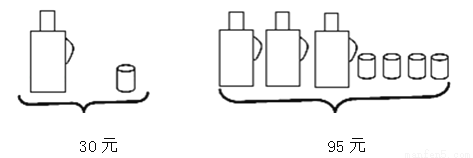
请根据图中提供的信息,回答下列问题:
一个水瓶与一个水杯分别是多少元?
查看答案和解析>>
科目:初中数学 来源:吉林省吉林市2016-2017七年级数学上期期末试卷 题型:单选题
当x=-1,y=1时ax+by-3=0,那么当x=1,y=-1时,ax+by-3的值是( )
A. -6 B. 0 C. 6 D. 9
A 【解析】【解析】 ∵当x=﹣1,y=1时,-a+b﹣3=0,即a﹣b=-3,∴当x=1,y=﹣1时,ax+by﹣3=a-b﹣3=﹣3﹣3=﹣6.故选A.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市姑苏区2017~2018学年第一学期八年级数学期末考试试卷 题型:解答题
(10分)已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源:江苏省苏州市姑苏区2017~2018学年第一学期八年级数学期末考试试卷 题型:填空题
若x2+mx+4是完全平方式,则m=_____.
±4 【解析】这里首末两项是2x和2这两个数的平方,那么中间一项为加上或减去2x和2积的2倍,依此求出m的值. 【解析】 ∵x2+mx+4是一个完全平方式, ∴这两个数2x和2, ∴mx=±2×2?x, 解得m=±4. 故答案为:±4.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市姑苏区2017~2018学年第一学期八年级数学期末考试试卷 题型:单选题
下列从左到右的运算是因式分解的是( )
A. 2a2﹣2a+1=2a(a﹣1)+1 B. (x﹣y)(x+y)=x2﹣y2
C. 9x2﹣6x+1=(3x﹣1)2 D. x2+y2=(x﹣y)2+2xy
C 【解析】A.没把一个多项式转化成几个整式积的形式,故A错误; B、是整式的乘法,故B错误; C、把一个多项式转化成几个整式积的形式,故C正确; D、没把一个多项式转化成几个整式积的形式,故D错误; 故选:C.查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第八章达标检测卷 题型:填空题
若2x5ayb+4与-x1-2by2a是同类项,则b=________.
-2 【解析】本题涉及同类项的概念:所含字母相同,相同字母的指数也相同,由此可得5a=1-2b,b+4=2a,将两式联立组成方程组,解出a,b的值,分别为a=1,b=-2 , 故答案为: b=-2.查看答案和解析>>
科目:初中数学 来源:2018年上海市奉贤区中考数学一模试卷 题型:解答题
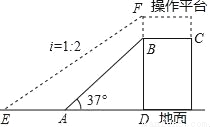
如图,为了将货物装入大型的集装箱卡车,需要利用传送带AB将货物从地面传送到高1.8米(即BD=1.8米)的操作平台BC上.已知传送带AB与地面所成斜坡的坡角∠BAD=37°.
(1)求传送带AB的长度;
(2)因实际需要,现在操作平台和传送带进行改造,如图中虚线所示,操作平台加高0.2米(即BF=0.2米),传送带与地面所成斜坡的坡度i=1:2.求改造后传送带EF的长度.(精确到0.1米)(参考数值:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, 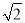 ≈1.41,
≈1.41, 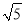 ≈2.24)
≈2.24)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com