
如图所示,已知∠1=∠2,那么下列结论正确的是( )
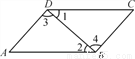
A. AB∥BC B. AB∥CD C. ∠C=∠D D. ∠3=∠4
B 【解析】∵∠1=∠2, ∴AB//CD(内错角相等,两直线平行), 故选B. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2016-2017学年山西农业大学附中七年级(下)第二次月考数学试卷 题型:解答题
长方形纸片的长是15㎝,长宽上各剪去两个宽为3㎝的长条,剩下的面积是原面积的 .求原面积.
.求原面积.

查看答案和解析>>
科目:初中数学 来源:2017年海南省文昌市中考数学模拟试卷 题型:单选题
一定质量的干木,当它的体积V=4m3时,它的密度ρ=0.25×103 kg/m3,则ρ与V的函数关系式是( )
A. ρ=1000V B. ρ=V+1 000 C. ρ=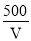 D. ρ=
D. ρ=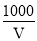
查看答案和解析>>
科目:初中数学 来源:2018年春北师大版七年级数学下册活页测试卷:期末测试 题型:填空题
如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的.若∠BAC=145°,则∠α=____.
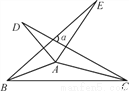
查看答案和解析>>
科目:初中数学 来源:2018年春北师大版七年级数学下册活页测试卷:期末测试 题型:单选题
通过计算几何图形面积可表示代数恒等式,上图可表示的代数恒等式是……( )
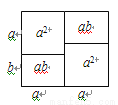
A.(a―b)2=a2―2ab+b2 B.(a+b)2=a2+2ab+b2
C.2a(a+b)=2a2+2ab D.(a+b)(a-b)=a2-b2
C 【解析】根据大长方形的面积等于四个小长方形的面积可得2a(a+b)=2a2+2ab,故选C查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是EC、DB的中点.求证:MN⊥BD.
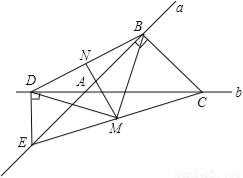
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
(1)作△ABC关于直线MN对称的△A′B′C′.
(2)如果网格中每个小正方形的边长为1,则△ABC的面积为 .
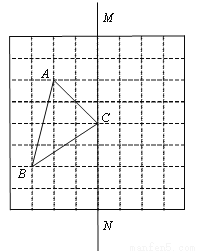
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
在以下节水、节能、回收、绿色食品四个标志中,是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:单选题
已知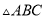 中,
中, 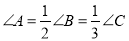 ,则它的三条边之比为( ).
,则它的三条边之比为( ).
A. 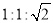 B.
B. 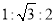 C.
C.  D.
D. 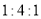
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com