
| 1 | 2 |
|
|
| 1 |
| 2 |
| 3 |
| 2 |
| DC |
| BC |
| PC |
| AC |
| 2 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
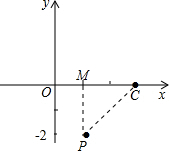
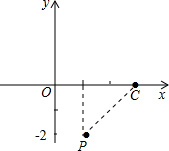
 锐角∠PCO与∠ACO的大小(不必证明),并写出此时点P的横坐标xp的取值范围.
锐角∠PCO与∠ACO的大小(不必证明),并写出此时点P的横坐标xp的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:
 种不同于(3)的正确证明吗?我们将对你的出色表现另外奖励3分.
种不同于(3)的正确证明吗?我们将对你的出色表现另外奖励3分.
| y=x2+px+q | p | q | △ | x1 | x2 | d | ||||||||
| y=x2-5x+6 | -5 | 6 | 1 | 2 | 3 | 1 | ||||||||
y=x2-
|
-
|
|
|
|||||||||||
| y=x2+x-2 | -2 | -2 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示对称轴为x=-
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示对称轴为x=-| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com