
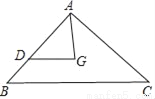
如图,在Rt△ABC中,∠BAC=90°,点G是重心,联结AG,过点G作DG∥BC,DG交AB于点D,若AB=6,BC=9,则△ADG的周长等于_____.
科目:初中数学 来源:海南省定安县2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
如图,把长方形 沿
沿 按图那样折叠后,A、B分别落在点G、H处,若∠1=50°,则∠AEF=( )
按图那样折叠后,A、B分别落在点G、H处,若∠1=50°,则∠AEF=( )
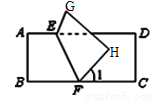
A. 110° B. 115° C. 120° D. 125°
B 【解析】【解析】 ∵四边形ABCD为长方形,∴AE∥BF,∠AEF+∠BFE=180°; 由折叠变换的性质得:∠BFE=∠HFE,而∠1=50°,∴∠BFE=(180°﹣50°)÷2=65°,∴∠AEF=180°﹣65°=115°.故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县七年级(上)期末数学试卷(五四学制) 题型:解答题
计算:(1)(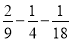 )×36
)×36
(2)(﹣1)4﹣36÷(﹣6)+3×(﹣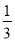 )
)
查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县七年级(上)期末数学试卷(五四学制) 题型:单选题
计算(﹣9)﹣(﹣3)的结果是( )
A. ﹣12 B. ﹣6 C. +6 D. 12
B 【解析】【解析】 (﹣9)﹣(﹣3)=﹣9+3=﹣6,故选B.查看答案和解析>>
科目:初中数学 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:解答题
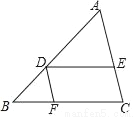
如图,在△ABC中,点D在边AB上,DE∥BC,DF∥AC,DE、DF分别交边AC、BC于点E、F,且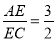 .
.
(1)求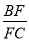 的值;
的值;
(2)联结EF,设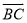 =
=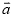 ,
, 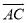 =
=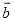 ,用含
,用含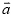 、
、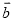 的式子表示
的式子表示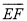 .
.
查看答案和解析>>
科目:初中数学 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:填空题
抛物线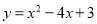 的顶点坐标是 _________.
的顶点坐标是 _________.
查看答案和解析>>
科目:初中数学 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:单选题
将抛物线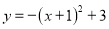 向右平移2个单位后得到的新抛物线的表达式为( )
向右平移2个单位后得到的新抛物线的表达式为( )
A. 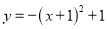 B.
B. 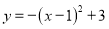
C. 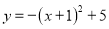 D.
D. 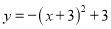
查看答案和解析>>
科目:初中数学 来源:北京市分校2017-2018学年度第一学期八年级数学期中试卷 题型:填空题
不改变分式的值,将分式 的分子、分母的各项系数都化为整数:______.
的分子、分母的各项系数都化为整数:______.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省九年级数学科期末检测模拟试卷 题型:解答题
如图,把一张直角三角形卡片ABC放在每格宽度为12mm的横格纸中,三个顶点恰好都落在横格线上,已知∠BAC=90°,∠α=36°,求直角三角形卡片ABC的面积(精确到1mm).(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
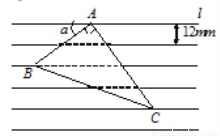
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com