练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    一水池的容积是90m3，现蓄水10m3，用水管以5m3/h的速度向水池注水，直到注满为止写出蓄水量V（m3）与注水时间t（h）之间的关系式（指出自变量t的取值范围）______．

    v=10+5t（0≤t≤16）． 【解析】试题解析：由蓄水量等于现蓄水量加注水量，得 V=5t+10， 由 解得 自变量t的取值范围： 故答案为：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：安徽省淮南市潘集区2017-2018学年八年级上学期第二次联考数学试卷 题型：填空题

    一个多边形内角和是一个四边形内角和的4倍，则这个多边形的边数是__________．

    10 【解析】试题分析：多边形的外角和是360度，多边形的外角和是内角和的4倍，则多边形的内角和是360×4=1440度，再由多边形的内角和列方程解答即可． 【解析】 设这个多边形的边数是n，由题意得， （n﹣2）×180°=360°×4 解得n=10． 故答案为：10．

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷（六） 题型：解答题

    如图，某办公楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，办公楼在建筑物的墙上留下高2米的影子CE，而当光线与地面夹角是45°时，办公楼顶A在地面上的影子F与墙角C有25米的距离（B，F，C在一条直线上）．

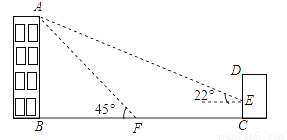
    （1）求办公楼AB的高度；

    （2）若要在A，E之间挂一些彩旗，请你求出A，E之间的距离．

    （参考数据：sin22°≈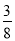，cos22°≈ 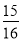，tan22°≈）

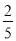    （1）教学楼的高20m；（2）A、E之间的距离约为48m． 【解析】（1）过点E作EM⊥AB于点M，设AB=x，在Rt△ABF中，由∠AFB=45°可知BF=AB=x， 在Rt△AEM中，利用锐角三角函数的定义求出x的值即可；（2）在Rt△AME中，根据cos22°=可得出结论． 【解析】 （1）过点E作EM⊥AB于点M，设AB=x， 在Rt△ABF中，∵∠AFB=45°...

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷（六） 题型：单选题

    下列说法中，正确的是（　　）

    A. 打开电视机，正在播广告，是必然事件

    B. 在连续5次的数学测试中，两名同学的平均分相同，方差较大的同学数学成绩更稳定

    C. 某同学连续10次抛掷质量均匀的硬币，3次正面向上，因此正面向上的概率是30%

    D. 从一个只装有白球的缸里摸出一个球，摸出的球是白球

    D 【解析】A、打开电视机，正在播广告，是随机事件，不是必然事件，故该选项错误； B、在连续5次的数学测试中，两名同学的平均分相同，方差较大的同学数学成绩不稳定，而不是稳定，故该选项错误； C、某同学连续10次抛掷质量均匀的硬币，3次正面向上，因此正面向上的概率是，不是30%，故该选项错误； D、从一个只装有白球的缸里摸出一个球，摸出的球是白球，是必然事件，故该选项正确，故...

    查看答案和解析>>

    科目：初中数学 来源：甘肃省张掖市高台县2016-2017学年八年级（上）期末数学试卷 题型：解答题

    如图，AD=CD，AC平分∠DAB，求证：DC∥AB．

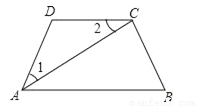
    证明见解析． 【解析】试题分析：由等腰三角形的性质和角平分线的定义可求得∠2=∠BAC，再根据平行线的判定可得出结论． 试题解析：证明：∵AD=CD， ∴∠1=∠2， ∵AC平分∠DAB， ∴∠1=∠BAC， ∴∠2=∠BAC， ∴DC∥AB．

    查看答案和解析>>

    科目：初中数学 来源：甘肃省张掖市高台县2016-2017学年八年级（上）期末数学试卷 题型：填空题

    已知三角形三边长分别是6，8，10，则此三角形的面积为________．

    24 【解析】试题解析： 此三角形为直角三角形, 此三角形的面积为: 故答案为:

    查看答案和解析>>

    科目：初中数学 来源：甘肃省张掖市高台县2016-2017学年八年级（上）期末数学试卷 题型：单选题

    下列命题是真命题的是（　　）

    A. 互补的两角相等，则这两角都是直角

    B. 直线是平角

    C. 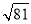的算术平方根是9

    D. 不相交的两条直线叫做平行线

    A 【解析】试题解析：A. 互补的两角相等，则这两角都是直角.是真命题. B.直线不是直角.是假命题. C. 的算术平方根是3.是假命题. D. 在同一平面内，不相交的两条直线叫做平行线.是假命题. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年七年级上期末复习检测数学试卷 题型：填空题

    计算：﹣3+（﹣4）=________

    -7 【解析】﹣3+（﹣4）=﹣（3+4）=﹣7， 故答案为：﹣7．

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷（三） 题型：解答题

    某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施.调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．

    （1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；（不要求写自变量的取值范围）

    （2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？

    （3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？

    （1）y=-x2+24x+3200； （2）每台冰箱应降价200元； （3）每台冰箱的售价降价150元时，商场的利润最大，最大利润是5000元． 【解析】试题分析：（1）根据总利润=单件利润×数量得出函数关系式；（2）将y=4800代入函数解析式，求出x的值，然后根据题意进行验根；（3）将二次函数进行配成顶点式，然后得出最值． 试题解析：（1）根据题意，得y=（2400﹣2...

    查看答案和解析>>

    同步练习册答案