解:(1)根据折叠的性质知:∠DA′B=∠OAB=90°,A′B=AB=4;
∵OC=A′B,∠DA′B=∠DCO=90°,∠ODC=∠BDA′,
∴△OCD≌△BA′D,
∴CD=A′D;
设CD=A′D=x,则BD=8-x;
Rt△A′BD中,由勾股定理得:x
2+4
2=(8-x)
2,
解得x=3;
故D(3,4);
设抛物线的解析式为:y=ax(x-8)
2,
则有:3a(3-8)=4,
a=-

;
∴y=-

x(x-8)
2=-

x
2+

x.
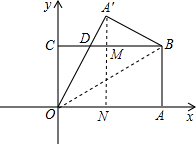
(2)过A′作x轴的垂线,交BC于M,交OA于N;
在Rt△A′BD中,A′M⊥BD,则:
A′M=A′D•A′B÷BD=

,
DM=A′D
2÷BD=

;
故CM=

,A′N=

,A′(

,

);
△A′AP中,AA′的长为定值,若周长最小,那么PA+PA′最小;
由于O、A关于抛物线的对称轴对称,则点P必为直线OA′与抛物线对称轴的交点;
易求得直线OA′:y=

x,
抛物线对称轴:x=4;
当x=4时,y=

,即P(4,

).
(3)假设存在符合条件的Q点,则有:
①D为△ADQ的直角顶点;
易求得直线AD的斜率:k=

=-

,
所以设直线DQ:y=

x+h,
则有:

×3+h=4,
解得h=

,
即y=

x+

,
当x=4时,y=

;
故Q(4,

);
②A为△ADQ的直角顶点,同①可求得Q(4,-5);
③Q为△ADQ的直角顶点,设Q(4,m),
则有:
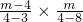
=-1,
即m
2-4m-4=0;
解得m=2±2

;
即Q(4,2+2

)或(4,2-2

);
综上可知:存在符合条件的Q点,且坐标为:
Q(4,-5)或(4,

)或(4,2+2

)或(4,2-2

).
分析:(1)欲求抛物线的解析式,就必须先求出D点的坐标,也就要求出CD的长;根据折叠的性质知:AB=A′B=OC=4,易证得△OCD≌△BA′D,那么CD=A′D,BD=BC-CD=8-CD,在Rt△A′BD中,利用勾股定理即可求出CD的长,从而得到点D的坐标,进而可由待定系数法求得抛物线的解析式.
(2)△PAA′中,AA′的长是定值,若此三角形的周长最小,那么PA+PA′的长最小,由于O、A关于抛物线的对称轴对称,那么P点必为直线OA′与抛物线对称轴的交点;过A′作x轴的垂线,交BC于M,交OA于N,在Rt△A′BD中,利用射影定理即可求得MD的长,利用直角三角形面积的不同表示方法即可求出A′N的长,由此求得点A′的坐标,进而得到直线OA′的解析式,联立抛物线对称轴方程,即可得到点P的坐标.
(3)此题应分三种情况考虑:
①点D为直角顶点,那么QD⊥AD,易得直线AD的解析式,由于QD⊥AD,那么直线QD和直线AD的斜率的乘积为-1,结合D点坐标即可求得直线DQ的解析式,联立抛物线的对称轴方程,即可求得点Q的坐标;
②点A为直角顶点,方法同①;
③点Q为直角顶点,设出点Q的坐标,由于DQ⊥AQ,那么两条直线的斜率乘积为-1,可据此列出关于Q点纵坐标的方程,从而求得点Q的坐标.
点评:此题考查了矩形的性质、图形的翻折变换、二次函数解析式的确定、平面展开-最短路径问题、直角三角形的判定、互相垂直的两直线的斜率关系等重要知识,(3)题中,一定要根据不同直角顶点来分类讨论,以免漏解.

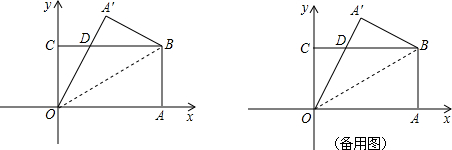
 ;
; x(x-8)2=-
x(x-8)2=- x2+
x2+ x.
x.
 ,
, ;
; ,A′N=
,A′N= ,A′(
,A′( ,
, );
); x,
x, ,即P(4,
,即P(4, ).
). =-
=- ,
, x+h,
x+h, ×3+h=4,
×3+h=4, ,
, x+
x+ ,
, ;
; );
);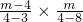 =-1,
=-1, ;
; )或(4,2-2
)或(4,2-2 );
); )或(4,2+2
)或(4,2+2 )或(4,2-2
)或(4,2-2 ).
).

 =2
=2
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.