
 如图,直线y=-mx-2与双曲线
如图,直线y=-mx-2与双曲线 交于点A,与x轴,y轴分别交于点B,C;AD⊥x轴于点D,tan∠DAB=
交于点A,与x轴,y轴分别交于点B,C;AD⊥x轴于点D,tan∠DAB= ;如果S△ADB=
;如果S△ADB= S△COB,那么k=________.
S△COB,那么k=________. -1
-1 上,所以只需求出点A的坐标即可.首先把B(-1,0)代入y=-mx-2,可求出m的值,得到一次函数的解析式,再通过证明△ADB∽△COB,根据相似三角形的性质求出OD的长,根据三角函数的知识求出AD的长,从而得到A点坐标,代入双曲线
上,所以只需求出点A的坐标即可.首先把B(-1,0)代入y=-mx-2,可求出m的值,得到一次函数的解析式,再通过证明△ADB∽△COB,根据相似三角形的性质求出OD的长,根据三角函数的知识求出AD的长,从而得到A点坐标,代入双曲线 ,得到k的值.
,得到k的值. ,
, .
.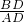 =
= ,
, .
. ,
, ),
), )•
)• =-
=- -1.
-1. 中k的几何意义.同时考查了相似三角形的性质及三角函数的知识,有一定的难度.
中k的几何意义.同时考查了相似三角形的性质及三角函数的知识,有一定的难度. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com