
 如图,A,B,C是三个村庄,它们恰好是正方形ABCD的三个顶点,现要在公路BD某处P的附近修建一座农产品收购站.当点P选在何处时AP+BP+CP的值最小?试利用图形的旋转,探索点P的位置.
如图,A,B,C是三个村庄,它们恰好是正方形ABCD的三个顶点,现要在公路BD某处P的附近修建一座农产品收购站.当点P选在何处时AP+BP+CP的值最小?试利用图形的旋转,探索点P的位置. 分析 将△ABP绕着点B逆时针旋转60°得到△A′BP′,则P′A′=PA,BP=BP′,∠PBP′=60°,于是得到△PBP′是等边三角形,根据等边三角形的性质得到PP′=PB,当A′,P′,P,C四点在同一条直线上时,AP+BP+CP的值最小;①将线段BA绕着点B逆时针旋转60°得到BA′,②连接A′C交BD于点P,则点P就是符合条件的点.
解答 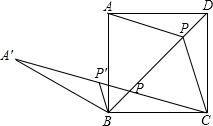 解:如图,将△ABP绕着点B逆时针旋转60°得到△A′BP′,则P′A′=PA,BP=BP′,∠PBP′=60°,
解:如图,将△ABP绕着点B逆时针旋转60°得到△A′BP′,则P′A′=PA,BP=BP′,∠PBP′=60°,
∴△PBP′是等边三角形,
∴PP′=PB,
∴当A′,P′,P,C四点在同一条直线上时,AP+BP+CP的值最小,
综上所述,点P的确定方法是:
①将线段BA绕着点B逆时针旋转60°得到BA′,
②连接A′C交BD于点P,则点P就是符合条件的点.
点评 本题考查了旋转的性质,辅助线的性质,等边三角形的判定和性质,正确的作出图形是解题的关键.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:解答题
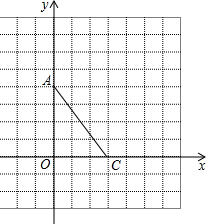 如图,在直角坐标系中,每个小格子单位长度均为1,点A、C分别在x轴、y轴的格点上.
如图,在直角坐标系中,每个小格子单位长度均为1,点A、C分别在x轴、y轴的格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ACEF的边长为2,以AC为一边在同侧做等腰三角形ABC,且∠BAC=150°,BC交AE于点D,下列结论:①EF=ED;②S△DEC=1+$\frac{\sqrt{3}}{3}$;③AD+CD=BD,④S△ABD=$\frac{\sqrt{3}}{3}$,其中正确结论的序号是②③④.
如图,正方形ACEF的边长为2,以AC为一边在同侧做等腰三角形ABC,且∠BAC=150°,BC交AE于点D,下列结论:①EF=ED;②S△DEC=1+$\frac{\sqrt{3}}{3}$;③AD+CD=BD,④S△ABD=$\frac{\sqrt{3}}{3}$,其中正确结论的序号是②③④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com