
如图, 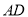 是
是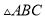 的角平分线,
的角平分线, 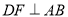 ,垂足为
,垂足为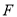 ,
, 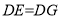 ,
, 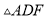 和
和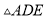 的面积分别为
的面积分别为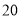 和
和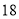 ,则
,则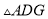 的面积为( ).
的面积为( ).
A. 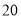 B.
B. 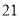 C.
C. 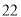 D.
D. 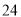
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:山东省2017-2018学年七年级12月月考数学试卷 题型:单选题
把弯曲的河道改直,能够缩短船舶航行的路程,这样做的道理是( )
A. 垂线段最短 B. 两点确定一条直线
C. 两点之间,直线最短 D. 两点之间,线段最短
D 【解析】把弯曲的河道改直,能够缩短船舶航行的路程,这样做的道理是两点之间,线段最短. 故选D.查看答案和解析>>
科目:初中数学 来源:浙江省杭州市西湖区绿城育华2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
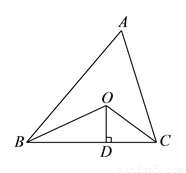
如图,已知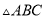 的周长是
的周长是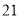 ,
, 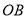 ,
, 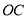 分别平分
分别平分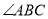 和
和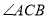 ,
, 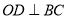 于
于 ,且
,且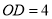 ,
, 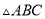 的面积是__________.
的面积是__________.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市余杭区英特外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
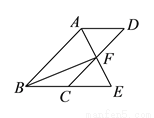
如图,四边形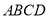 ,
, 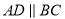 ,
, 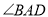 的角平分线
的角平分线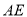 交
交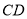 于点
于点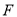 ,交
,交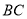 的延长线于点
的延长线于点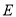 ,若点
,若点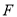 是
是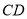 的中点,求证:
的中点,求证: 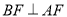 .
.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市余杭区英特外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
在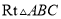 中,
中, 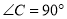 ,斜边长为
,斜边长为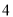 ,
, 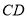 为
为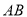 边上中线,则
边上中线,则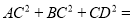 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市余杭区英特外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
下列四组条件中,能够判定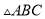 和
和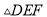 全等的是( ).
全等的是( ).
A. 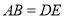 ,
, 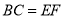 ,
, 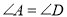 B.
B. 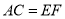 ,
, 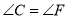 ,
, 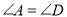
C. 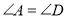 ,
, 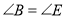 ,
, 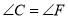 D.
D. 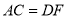 ,
, 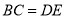 ,
, 
查看答案和解析>>
科目:初中数学 来源:河南省邓州市2018届九年级上学期期中质量评估---数学试卷word版 题型:解答题
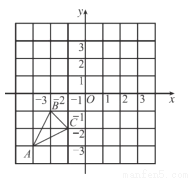
如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上的三点.
(1)请画出△ABC关于x轴对称的△A₁B₁C₁;
(2)请写出B点关于y轴对称的点B2的坐标;若将点B向上平移h个单位,欲使其落在△A1B1C1内部,指出h的取值范围.
查看答案和解析>>
科目:初中数学 来源:河南省邓州市2018届九年级上学期期中质量评估---数学试卷word版 题型:单选题
下列二次根式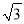 ,
, 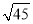 ,
, 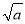 ,
, 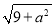 中,最简二次根式的个数是 ( )
中,最简二次根式的个数是 ( )
A. 1 B. 2 C. 3 D. 4
C 【解析】【解析】 =.而, , 是最简二次根式.故选C.查看答案和解析>>
科目:初中数学 来源:北京市延庆县第一学区2017-2018学年八年级(上)期中数学试卷 题型:单选题
下列各式中,正确的是( )
A. 2<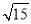 <3 B. 3<
<3 B. 3<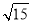 <4 C. 4<
<4 C. 4<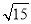 <5 D. 14<
<5 D. 14<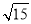 <16
<16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com