

| 解:(1)Q(1,0); 点P运动速度每秒钟1个单位长度。 | |
| (2)过点作BF⊥y轴于点F,BE⊥x轴于点E,则BF=8,OF=BE=4, ∴AF=10-4=6, 在Rt△AFB中,  , ,过点C作CG⊥x轴于点G,与FB的延长线交于点H, ∵  , ,∴△ABF≌△BCH, ∴BH=AF=6,CH=BF=8, ∴OG=FH=8+6=14,CG=8+4=12, ∴所求C点的坐标为(14,12)。 |
 |
| (3)过点P作PM⊥y轴于点M,PN⊥轴于点N, 则△APM∽△ABF, ∴  ,即 ,即 , ,∴  , , , ,∴PN=OM=10-  ,ON=PM= ,ON=PM= , ,设△OPQ的面积为S(平方单位),  ,(0≤t≤10) ,(0≤t≤10)∵  <0, <0,∴当  时,△OPQ的面积最大, 时,△OPQ的面积最大,此时P的坐标为(  , , )。 )。 |


科目:初中数学 来源: 题型:
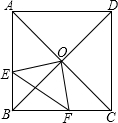 已知,如图,在正方形ABCD中,O是对角线AC、BD的交点,过O作OE⊥OF,分别交AB、BC于点E、F,若AE=4,CF=3,则四边形OEBF的面积为
已知,如图,在正方形ABCD中,O是对角线AC、BD的交点,过O作OE⊥OF,分别交AB、BC于点E、F,若AE=4,CF=3,则四边形OEBF的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
 10、如图,在正方形ABCD中,AB=4,点O在AB上,且OB=1,点P是BC上一动点,连接OP,将线段OP绕点D逆时针旋转90°得到线段OQ.要使点Q恰好落在AD上,则BP的长是( )
10、如图,在正方形ABCD中,AB=4,点O在AB上,且OB=1,点P是BC上一动点,连接OP,将线段OP绕点D逆时针旋转90°得到线段OQ.要使点Q恰好落在AD上,则BP的长是( )查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
| 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 3 |
5
| ||
| 2 |
5
| ||
| 2 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com