已知△ABC和△A′B′C′,∠C=∠C′=90°,AC=A′C′,要判定△ABC≌△A′B′C′,必须添加的条件为①________或②________或③________或④________.
AB=A′B′ ∠A=∠A′ ∠B=∠B′ BC=B′C′
分析:本题要判定△ABC≌△A'B'C',已知∠C=∠C'=90°,AC=A'C',具备了一组边和一组角对应相等,故可添加AB=A′B′、∠A=∠A′、∠B=∠B′、BC=B′C′后分别根据HL、ASA、AAS、SAS判定两三角形全等.
解答:添加AB=A′B′;
∵∠C=∠C'=90°,AC=A'C',AB=A′B′
∴△ABC≌△A'B'C'(HL);
添加∠A=∠A′;
∵∠C=∠C'=90°,AC=A'C',∠A=∠A′
∴△ABC≌△A'B'C'(ASA);
添加∠B=∠B′;
∵∠C=∠C'=90°,AC=A'C',∠B=∠B′
∴△ABC≌△A'B'C'(AAS);
添加BC=B′C′;
∵∠C=∠C'=90°,AC=A'C',BC=B′C′
∴△ABC≌△A'B'C'(SAS).
故答案为:AB=A′B′、∠A=∠A′、∠B=∠B′、BC=B′C′.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.



 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
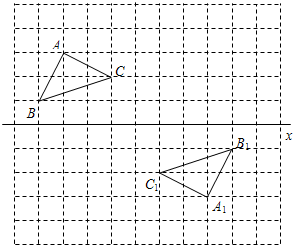 如图,在正方形网格中每个小正方形的边长都是单位1,已知△ABC和△A1B1C1关于点O成中心对称,点O直线x上.
如图,在正方形网格中每个小正方形的边长都是单位1,已知△ABC和△A1B1C1关于点O成中心对称,点O直线x上.