
 上运动(不与点B、C重合),过
上运动(不与点B、C重合),过 点D作DE∥BC交AC的延长线于点E,连接AD、CD
点D作DE∥BC交AC的延长线于点E,连接AD、CD 的中点时,DE与⊙O相切.
的中点时,DE与⊙O相切. 的中点,
的中点, ∴DE与⊙O相切;
∴DE与⊙O相切; ×360°=120°,∠ACB=60°,
×360°=120°,∠ACB=60°, ∠BAC=30°,
∠BAC=30°, =2
=2 ,
, AC•CD=
AC•CD= ×6×2
×6×2 =6
=6 .
. 的中点时,由垂径定理,可得OD⊥BC,又由DE∥BC,即可得OD⊥DE,即可证得DE与⊙O相切;
的中点时,由垂径定理,可得OD⊥BC,又由DE∥BC,即可得OD⊥DE,即可证得DE与⊙O相切;

科目:初中数学 来源: 题型:
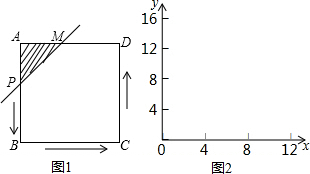 动的路程为X,请解答下列问题:
动的路程为X,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•营口)如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.
(2012•营口)如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com