
如图,已知⊙O的半径为2,弦BC的长为 ,点A为弦BC所对优弧上任意一点(B,C两点除外).
,点A为弦BC所对优弧上任意一点(B,C两点除外).
 (1)求∠BAC的度数;
(1)求∠BAC的度数;
(2)求△ABC面积的最大值.
(参考数据: ,
, ,
, .)
.)
解:(1) 解法一
连接OB,OC,过O作OE⊥BC于点E.
∵OE⊥BC,BC= ,
,
∴ . ………………1分
. ………………1分
 在Rt△OBE中,OB=2,∵
在Rt△OBE中,OB=2,∵ ,
,
∴ , ∴
, ∴ ,
,
∴ .
………………4分
.
………………4分
解法二
连接BO并延长,交⊙O于点D,连接CD.
∵BD是直径,∴BD=4, .
.
在Rt△DBC中, ,
,
∴ ,∴
,∴ .………………4分
.………………4分
(2) 解法一
因为△ABC的边BC的长不变,所以当BC边上的高最大时,△ABC的面积最大,此时点A落在优弧BC的中点处. ………………5分
过O作OE⊥BC于E,延长EO交⊙O于点A,则A为优弧BC的中点.连接AB,AC,则AB=AC, .
.
 在Rt△ABE中,∵
在Rt△ABE中,∵ ,
,
∴ ,
,
∴S△ABC= .
.
答:△ABC面积的最大值是 .
………………7分
.
………………7分
解法二
因为△ABC的边BC的长不变,所以当BC边上的高最大时,△ABC的面积最大,此时点A落在优弧BC的中点处. ………………5分
过O作OE⊥BC于E,延长EO交⊙O于点A,则A为优弧BC的中点.连接AB,AC,则AB=AC.
∵ , ∴△ABC是等边三角形.
, ∴△ABC是等边三角形.
在Rt△ABE中,∵ ,
,
∴ ,
,
∴S△ABC= .
.
答:△ABC面积的最大值是 . ………………7分
. ………………7分
【解析】略


科目:初中数学 来源: 题型:
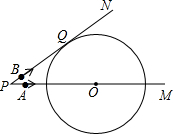 P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts.
P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:
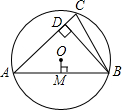 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,弦AB=8,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,弦AB=8,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )| A、0.6 | B、0.8 | C、0.5 | D、1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.
(2013•新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.查看答案和解析>>
科目:初中数学 来源: 题型:
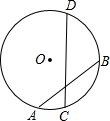 如图,已知⊙O的半径为5,两弦AB、CD相交于AB中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )
如图,已知⊙O的半径为5,两弦AB、CD相交于AB中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com