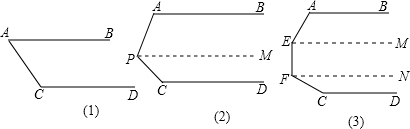
解:(1)∵AB∥CD,∴∠A+∠C=180°(两直线平行,同旁内角互补);
(2)过点P作一条直线PM平行于AB,
∵AB∥CD,
∵AB∥PM,CD∥PM,
∴∠A+∠APM=180°,∠MPC+∠C=180°,
∴∠A+∠APC+∠C=360°;
(3)分别过点E、F作EM、FN平行于AB,
∵AB∥CD,
∵AB∥EM∥FN∥CD,
∴∠A+∠AEM=180°,∠MEF+∠EFN=180°,∠NFC+∠C=180°;
∴∠A+∠AEF+∠EFC+∠C=540°;
(4)由以上规律,有两个角时,和为180°;
有三个角时和为360°;
有四个角时和为540°…
故可得有n个角时,和为180°(n-1).
分析:(1)据两直线平行,同旁内角互补可得∠A+∠C=180°;
(2)沿P作一条平行AB、CD的平行线PM,由两直线平行,同旁内角互补可得∠A+∠APM=180°,∠MPC+∠C=180°,故∠A+∠APC+∠C=360°;
(3)根据第二题,同理可得∠A+∠AEF+∠EFC+∠C=540°;
(4)由以上规律,有两个角时,和为180°;有三个角时和为360°;有四个角时和为540°…故可得有n个角时,和为180°(n-1).
点评:本题主要考查两直线平行,同旁内角互补的性质,并考查学生通过计算总结规律的能力,是一道好题.

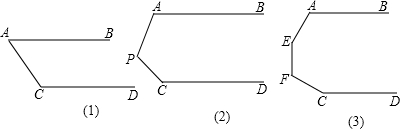
 解:(1)∵AB∥CD,∴∠A+∠C=180°(两直线平行,同旁内角互补);
解:(1)∵AB∥CD,∴∠A+∠C=180°(两直线平行,同旁内角互补);

 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=