
 ∠A;
∠A; ∠A.
∠A. 
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
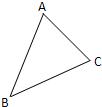 25、画图并讨论:
25、画图并讨论:查看答案和解析>>
科目:初中数学 来源: 题型:
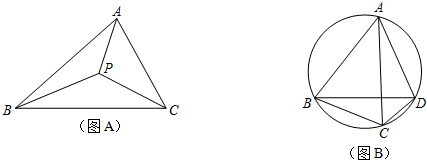
 |
| BC |
 |
| BC |
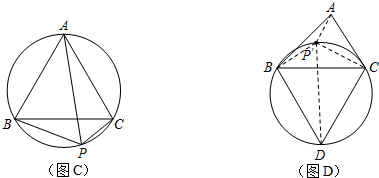
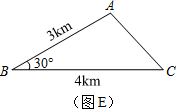
查看答案和解析>>
科目:初中数学 来源: 题型:
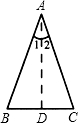 “等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合”的定理是将“等腰三角形”作为一个不变的已知条件参与组合得到的三个真命题,在学习了等腰三角形的判定后,可将该定理作如下的引伸.
“等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合”的定理是将“等腰三角形”作为一个不变的已知条件参与组合得到的三个真命题,在学习了等腰三角形的判定后,可将该定理作如下的引伸.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com