
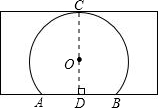
 如图,数学学习小组的同学在清晏院内发现一个圆形拱门,经测量,路面AB宽为2m,净高CD为4m,则圆形拱门所在圆的半径为________m.
如图,数学学习小组的同学在清晏院内发现一个圆形拱门,经测量,路面AB宽为2m,净高CD为4m,则圆形拱门所在圆的半径为________m. 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
 定义:三边长和面积都是整数的三角形称为“整数三角形”.
定义:三边长和面积都是整数的三角形称为“整数三角形”.查看答案和解析>>
科目:初中数学 来源: 题型:
 定义:三边长与面积都是整数的三角形称为“整数三角形”.数学学习小组的同学们从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾顺次连接组成三角形,进行探究活动.如图是小亮同学用12根火柴棒,摆成如图所示的“整数三角形”.
定义:三边长与面积都是整数的三角形称为“整数三角形”.数学学习小组的同学们从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾顺次连接组成三角形,进行探究活动.如图是小亮同学用12根火柴棒,摆成如图所示的“整数三角形”.查看答案和解析>>
科目:初中数学 来源: 题型:
 一天,数学学习小组的三名同学小聪、小明、小雨发现一把30°的直角尺斜靠在教室的墙角(如图,△ABC中的直角边BC长为50cm),小聪提议针对这一现象,每人提出一个数学问题.
一天,数学学习小组的三名同学小聪、小明、小雨发现一把30°的直角尺斜靠在教室的墙角(如图,△ABC中的直角边BC长为50cm),小聪提议针对这一现象,每人提出一个数学问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com