
如图:抛物线 与x 轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C。
与x 轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C。
⑴求抛物线的对称轴和点B的坐标;
⑵过点C作CP⊥对称轴于点P,连结BC交对称轴于点D,连结AC、BP,且  ,求抛物线的解析式;
,求抛物线的解析式;
⑶在⑵的条件下,设抛物线的顶点为G,连结BG、CG、求 BCG的面积。
BCG的面积。

⑴对称轴是x=- …………………2′
…………………2′
∵点A(1,0)且点A、B关于x=2对称
∴点B(3,0) …………4′
⑵点A(1,0),B(3,0)
∴ AB=2
∵ CP⊥对称轴于P
∴ CP∥AB
∵ 对称轴是x=2
∴ AB∥CP且AB=CP
∴ 四边形ABPC是平行四边形 …5′
设点C(0,x) x<0
在Rt AOC中,AC=
AOC中,AC=
∴ BP=
在Rt BOC中,BC=
BOC中,BC=
∵ 
∴ BD=

∵ ∠BPD=∠PCB 且∠PBD=∠CBP
∴  BPD~
BPD~ BCP
…………………7′
BCP
…………………7′
∴ 
即

∴ 

∵ 点C在y轴的负半轴上 ∴ 点C(0, )…8′
)…8′
∴ 
∵ 过点(1,0)
∴ 


解析式是: …………………9′
…………………9′
⑶ 当x=2时,
顶点坐标G是(2, )
…………………10′
)
…………………10′
设CG的解析式是:
(0, )(2,
)(2, )
)
∴ 
∴ …………………11′
…………………11′
设CG与x轴的交点为H
令y=0 则 得
得 
即H( ,0)
…………………12′
,0)
…………………12′
∴ BH= =
=




 …………………13′
…………………13′
(本题若有其它解法,正确给满分)
【解析】略


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
| 3 | 2 |
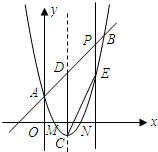 作x轴的垂线交抛物线于点E,使四边形DCEP为平行四边形?若存在,请求出该平行四边形的面积;若不存在,说明理由.
作x轴的垂线交抛物线于点E,使四边形DCEP为平行四边形?若存在,请求出该平行四边形的面积;若不存在,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
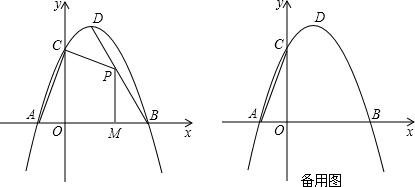
查看答案和解析>>
科目:初中数学 来源: 题型:
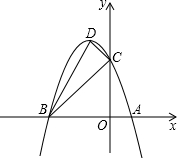 (2013•营口)如图,抛物线与x轴交于A(1,0)、B(-3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
(2013•营口)如图,抛物线与x轴交于A(1,0)、B(-3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与x轴交于A(-2,0),B(6,0)两点,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A(-2,0),B(6,0)两点,与y轴交于点C(0,-4).查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com