
求证:(1)OE<OF;(2)∠AOB>∠COD;(3)![]() >
>![]() .
.

| 延长OE、OF分别交⊙O于M、N.
∵OE⊥AB,OF⊥CD,∴E、F分别是AB、CD的中点. M、N分别是 ∴2∠BOM=∠AOB,2∠DON=∠COD. ∴ (1) 在Rt△BOE和Rt△DOF中, ∵OE= ∵AB>CD,∴ 又OB=OD,∴OB2-BE2<OD2-DF2,∴OE<OF. (2) 根据锐角三角函数定义,知sinBOE= ∵ ∴sinBOE>sinDOF ∵∠BOE和∠DOF都是锐角,∴∠BOE>∠DOF. ∴∠AOB>∠COD. (3)∵∠AOB>∠COD,∴ ∴
|


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
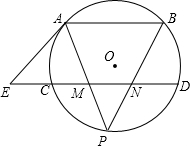 如图,已知AB、CD是⊙O的两条平行弦,过A点的⊙O的切线AE和DC的延长线交于E点,P为弧
如图,已知AB、CD是⊙O的两条平行弦,过A点的⊙O的切线AE和DC的延长线交于E点,P为弧 | CD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com