练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．分式$\frac{6{x}^{2}+12x+10}{{x}^{2}+2x+2}$的最小值是4．

    分析 首先将分式变形为6-$\frac{2}{（x+1）^{2}+1}$，依据代数式可知当x=-1时，分式有最小值．

    解答 解：$\frac{6{x}^{2}+12x+10}{{x}^{2}+2x+2}$=$\frac{6{x}^{2}+12x+12-2}{{x}^{2}+2x+2}$=6-$\frac{2}{{x}^{2}+2x+2}$=6-$\frac{2}{（x+1）^{2}+1}$．
    ∴当x=-1时，分式$\frac{6{x}^{2}+12x+10}{{x}^{2}+2x+2}$有最小值，分式的最小值=6-2=4．
    故答案为：4．

    点评 本题主要考查的是二次函数的最值问题，能够将分式进行适当变形是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    14．已知x＞2，则下列变形正确的是（　　）
    A．-x＜2B．若y＞2，则x-y＞0C．-$\frac{1}{2}$x+2＜1D．若y＞2，则$\frac{x}{y}＞1$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．（1）若A=x2+4xy+y2-4，B=4x+4xy-6y-25，则比较A、B的大小关系；
    （2）若（x+2）（x2+mx+4）的展开式中不含有x的二次项，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．某制造企业有一座对生产设备进行水循环冷却的冷却塔，冷却塔的顶部有一个进水口，3小时恰好可以注满这座空塔，底部有一个出水口，7小时恰好可以放完满塔的水．为了保证安全，塔内剩余水量不得少于全塔水量的$\frac{1}{4}$，出水口一直打开，保证水的循环，进水口根据水位情况定时对冷却塔进行补水．假设每次恰好在剩余水量为满水量的m倍时开始补水，补满后关闭进水口．
    （1）当m=$\frac{1}{4}$时，请问：两次补水之间相隔多长时间？每次补水需要多长时间？
    （2）能否找到适当的m值，使得两次补水的间隔时间和每次的补水时间一样长？如果能，请求出m值；如果不能，请你分析两次补水的间隔时间和每次的补水时间之间的数量关系，并表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．分解因式：已知m是正整数，且m4-16m2+100是质数，则m的算术平方根是$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．O是△ABC内一点，且到三边的距离相等，若∠A=56°，则∠BOC=118°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．一个两位数，十位上的数字是x，个位上的数字是y，把这个两位数十位上数字与个位上数字调换位置后的两位数用代数式表示为（　　）
    A．yxB．xyC．10y+xD．10x+y

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．小明在荡秋千时，发观秋千在静止时，秋千离地面3dm（EF=3dm），荡起的水平距离为13dm（BC=13dm）时，离地面8dm（BD=8dm），求秋千的绳索AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

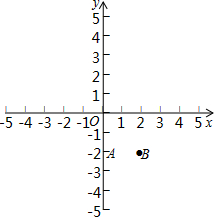    5．在如图的平面直角坐标系xOy中，抛物线y=2x2+bx+c经过点A（0，-2），B（2，-2）．
    （1）该抛物线的对称轴为直线x=1，若点（-3，m）与点（3，n）在该抛物线上，则m＞n（填“＞”、“=”或“＜”）；
    （2）求抛物线的函数表达式及顶点坐标，并画出图象；
    （3）设点C的坐标为（-3，-4），点C关于原点的对称点为C′，点D是抛物线对称轴上一动点，记抛物线在直线CC′以下部分为图象g，若直线CD与图象g有公共点，结合函数图象，求点D纵坐标t的取值范围．

    查看答案和解析>>

    同步练习册答案