
 如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O,A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,当点A在运动过程中,⊙P与菱形OABC的边所在直线相切时,t=________.
如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O,A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,当点A在运动过程中,⊙P与菱形OABC的边所在直线相切时,t=________. 或
或 或
或
 ,表示出OC,等于1+t列出关于t的方程,求出方程的解即可得到t的值;②当圆P与OA,即与x轴相切时,过P作PE垂直于OC,又PC=PO,利用三线合一得到E为OC的中点,OE为OC的一半,而OE=OPcos30°,列出关于t的方程,求出方程的解即可得到t的值;③当圆P与AB所在的直线相切时,设切点为F,PF与OC交于点G,由切线的性质得到PF垂直于AB,则PF垂直于OC,由CD=FG,在直角三角形OCD中,利用锐角三角函数定义由OC表示出CD,即为FG,在直角三角形OPG中,利用OP表示出PG,用PG+GF表示出PF,根据PF=PC,表示出PC,过C作CH垂直于y轴,在直角三角形PHC中,利用勾股定理列出关于t的方程,求出方程的解即可得到t的值,综上,得到所有满足题意的t的值.
,表示出OC,等于1+t列出关于t的方程,求出方程的解即可得到t的值;②当圆P与OA,即与x轴相切时,过P作PE垂直于OC,又PC=PO,利用三线合一得到E为OC的中点,OE为OC的一半,而OE=OPcos30°,列出关于t的方程,求出方程的解即可得到t的值;③当圆P与AB所在的直线相切时,设切点为F,PF与OC交于点G,由切线的性质得到PF垂直于AB,则PF垂直于OC,由CD=FG,在直角三角形OCD中,利用锐角三角函数定义由OC表示出CD,即为FG,在直角三角形OPG中,利用OP表示出PG,用PG+GF表示出PF,根据PF=PC,表示出PC,过C作CH垂直于y轴,在直角三角形PHC中,利用勾股定理列出关于t的方程,求出方程的解即可得到t的值,综上,得到所有满足题意的t的值. ∵OA=1+t,四边形OABC为菱形,
∵OA=1+t,四边形OABC为菱形, ,
, -1;
-1; 切点为O,PC=OP=3,
切点为O,PC=OP=3, OC,
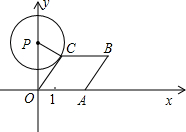
OC,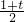 =OPcos30°=
=OPcos30°= ,
, -1;
-1;
 (1+t),
(1+t), (1+t)=
(1+t)= +
+ (1+t),
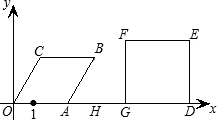
(1+t), )2+(
)2+( -3)2=(
-3)2=( +
+ )2,
)2, (t+1)+27=0,
(t+1)+27=0, ±6
±6 ,
, -6
-6 -1<0,
-1<0, +6
+6 -1,
-1, -1或3
-1或3 -1或9
-1或9 +6
+6 -1.
-1. -1或3
-1或3 -1或9
-1或9 +6
+6 -1.
-1.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,求:
A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,求:查看答案和解析>>
科目:初中数学 来源: 题型:
 ,求出t的值;若不存在,请说明理由.
,求出t的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,求出t的值;若不存在,请说明理由.
,求出t的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2010年江苏省无锡市惠山区八校联考中考适应性训练数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:第26章《圆》中考题集(48):26.5 直线与圆的位置关系(解析版) 题型:解答题
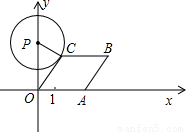
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com