练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，已知P是等边△ABC内任意一点，过点P分别向三边作垂线，垂足分别是D、E、F，试证明PD＋PE＋PF是不变的值．

    答案：略
    解析：

    证明：过点A作AH⊥BC于H，连接PA、PB、PC．

    ∵，

    即．

    又∵AB=BC=AC，

    ∴AH=PD＋PE＋PF．

    ∴PD＋PE＋PF的值是等边△ABC的高，是不变的值．


    提示：

    由于△ABC是等边三角形，故它的三边AB=BC=AC，而PD、PE、PF恰好是这三边上的高，因此本题可想到用三角形的面积法解题．连接PA、PB、PC，把△ABC分成了三个三角形△PAB、△PBC、△PAC，这三个三角形面积的和正好等于等边△ABC的面积，由面积之间的关系即可说明PD＋PE＋PF等于△ABC的高，即为定值．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

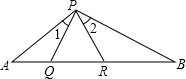    精英家教网如图，已知A是等边三角形PQR的边RQ的延长线上的点，B是QR延长线上的点，
    （1）若∠1+∠2=60°，求证：QR2=AQ•BR．
    （2）若AQ=
    12
    QR    ，当RB与QR满足什么条件时，△BRP∽△PQA？
    （3）△BPQ有可能与△PQA相似吗？若可能相似，说明应满足什么条件；若不可能相似，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•襄城区模拟）如图，已知△ABC是等边三角形，D、E分别在边BC、AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF、BE和CF．
    （1）求证：△BCE≌△FDC；
    （2）判断四边形ABDF是怎样的四边形，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•奉贤区二模）如图，已知△ABC是等边三角形，点D是BC延长线上的一个动点，以AD为边作等边△ADE，过点E作BC的平行线，分别交AB，AC的延长线于点F，G，联结BE．
    （1）求证：△AEB≌△ADC；
    （2）如果BC=CD，判断四边形BCGE的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

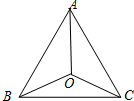    如图，已知O是等边三角形△ABC内一点，∠AOB、∠BOC、∠AOC的度数之比为6：5：4，在以OA、OB、OC为边的三角形中，此三边所对的角的度数是
    36°或60°或84°
    36°或60°或84°
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

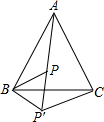    如图，已知P是等边△ABC内的一点，连接AP、BP，将△ABP旋转后能与△CBP′重合，根据图形回答：（1）旋转中心是哪一点？
    （2）旋转角是几度？
    （3）连接PP′后，△BPP′是什么三角形？

    查看答案和解析>>

    同步练习册答案