
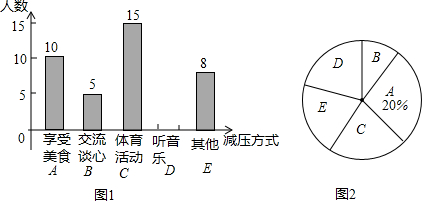
分析 (1)利用“享受美食”的人数除以所占的百分比计算即可得解;
(2)求出听音乐的人数即可补全条形统计图;由C的人数即可得到所对应的圆心角度数;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与选出两名同学都是女生的情况,再利用概率公式即可求得答案.
解答 解:
(1)由题意可得总人数为10÷20%=50名;
(2)听音乐的人数为50-10-15-5-8=12名,“体育活动C”所对应的圆心角度数=$\frac{15}{50}×360°$=108°,
补全统计图得: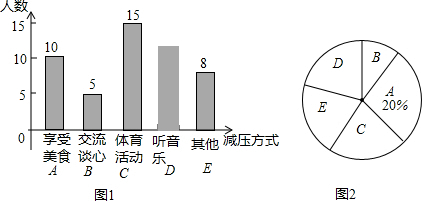
(3)画树状图得:
∵共有20种等可能的结果,选出都是女生的有2种情况,
∴选取的两名同学都是女生的概率=$\frac{2}{20}$=$\frac{1}{10}$.
点评 本题考查的是用列表法或画树形图求随机事件的概率,条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:解答题
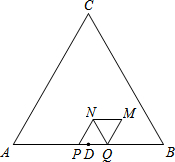 如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3).
如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC,以边BC为直径的⊙O与边AB,AC分别交于D,F两点,过点D作⊙O的切线DE,使DE⊥AC于E.
如图,△ABC中,AB=AC,以边BC为直径的⊙O与边AB,AC分别交于D,F两点,过点D作⊙O的切线DE,使DE⊥AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
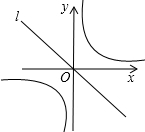 如图,已知直线l:y=-x,双曲线y=$\frac{1}{x}$,在l上取一点A(a,-a)(a>0),过A作x轴的垂线交双曲线于点B,过B作y轴的垂线交l于点C,过C作x轴的垂线交双曲线于点D,过D作y轴的垂线交l于点E,此时E与A重合,并得到一个正方形ABCD,若原点O在正方形ABCD的对角线上且分这条对角线为1:2的两条线段,则a的值为$\sqrt{2}$或$\frac{\sqrt{2}}{2}$.
如图,已知直线l:y=-x,双曲线y=$\frac{1}{x}$,在l上取一点A(a,-a)(a>0),过A作x轴的垂线交双曲线于点B,过B作y轴的垂线交l于点C,过C作x轴的垂线交双曲线于点D,过D作y轴的垂线交l于点E,此时E与A重合,并得到一个正方形ABCD,若原点O在正方形ABCD的对角线上且分这条对角线为1:2的两条线段,则a的值为$\sqrt{2}$或$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com