
 已知三个边长分别为1,2,3的正方形如图排成一排,图中四边形ABCD的周长是________.
已知三个边长分别为1,2,3的正方形如图排成一排,图中四边形ABCD的周长是________. +
+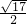
 MN=
MN= ,进而可得出CD的长,连接BC,过点C作CE⊥AB于点E,可得出BE及CE的长,利用勾股定理可求出BC的长,进而得出结论.
,进而可得出CD的长,连接BC,过点C作CE⊥AB于点E,可得出BE及CE的长,利用勾股定理可求出BC的长,进而得出结论.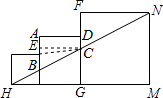 解:∵三个正方形的边长分别为1,2,3,
解:∵三个正方形的边长分别为1,2,3, MN=
MN= ,
, =
= ,
, ,AD=2,
,AD=2, =
= ,
, =
=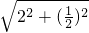 =
=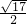 ,
, +
+ +2=
+2= +
+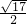 .
.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com