解:(1)如图1:当AB为梯形的底时,PQ∥AB,
∴Q在CP上,
∵△APQ是等边三角形,CP∥x轴,
∴AC垂直平分PQ,
∵A(0,2),C(0,4),
∴AC=2,
∴PC=AC•tan30°=2×

=

,
∴当AB为梯形的底时,点P的横坐标是:

;
(2)如图2,当AB为梯形的腰时,AQ∥BP,
∴Q在y轴上,
∴BP∥y轴,

∵CP∥x轴,
∴四边形ABPC是平行四边形,
∴CP=AB=2

,
如图3,当C与P重合时,
∵A(0,2)、B(

,2),
∴tan∠APB=
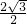
=

,
∴∠APQ=60°,
∵△APQ是等边三角形,
∴∠PAQ=60°,
∴∠ACB=∠PAQ,
∴AQ∥BP,
∴当C与P重合时,四边形ABPQ以AB为腰的梯形,
此时点P的横坐标为0;
∴当AB为梯形的腰时,点P的横坐标是:0或2

.
故答案为:(1)

,(2)0或2

.
分析:首先根据题意画出符合题意的图形,(1)当AB为梯形的底时,PQ∥AB,可得Q在CP上,由△APQ是等边三角形,CP∥x轴,即可求得答案;
(2)当AB为梯形的腰时,AQ∥BP,易得四边形ABPC是平行四边形,即可求得CP的长,继而可求得点P的横坐标.
点评:此题考查了梯形的性质与等边三角形的性质.此题难度适中,解题的关键是根据题意画出符合要求的图形,然后利用数形结合思想求解.

 ,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连
,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连 接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则:
接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则: =
= ,
, ;
;
 ,
, ,2),
,2),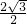 =
= ,
, .
. ,(2)0或2
,(2)0或2 .
.

 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( ) 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设