练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，船从点B沿BD向正东方向航行，在B点测得灯塔A在北偏东．航行0.5 h后，到达点C，测得灯塔A在北偏东方向上．求灯塔A对B，C两点张角∠BAC的度数．

    答案：
    解析：

    　　解：由题意得∠ABC＝－＝，∠ACB＝＋＝，所以∠BAC＝－(∠ABC＋∠ACB)＝，故A对B，C两点张角∠BAC为．

    　　解题指导：△ABC中，如能求出∠ABC，∠ACB度数，就能求出∠BAC的度数．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    62、如图所示，一艘船从A点出发，沿东北方向航行至B，再从B点出发沿南偏东15°方向航行至C点，则∠ABC等于多少
    60
    度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

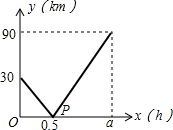    （2013•溧水县一模）在一条直线上依次有A、B、C三个海岛，某海巡船从A岛出发沿直线匀速经B岛驶向C岛，执行海巡任务，最终达到C岛．设该海巡船行驶x（h）后，与B港的距离为y（km），y与x的函数关系如图所示．
    （1）图中点P的坐标为（0.5，0），请解释该点坐标所表示的实际意义；
    （2）填空：A、C两港口间的距离为
    120
    120
    km，a=
    2
    2
    ；
    当0＜x≤0.5时，y与x的函数关系式为：
    y=-60x+30
    y=-60x+30
    ；
    当0.5＜x≤a时，y与x的函数关系式为：
    y=60x-30
    y=60x-30
    ；
    （3）在B岛有一不间断发射信号的信号发射台，发射的信号覆盖半径为24km，求该海巡船能接受到该信号的时间有多长？
    （4）请你根据以上信息，针对A岛，就该海巡船航行的“路程”，提出一个问题，并写出解答过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    两艘渔船同时从O点出发，甲船以40海里/小时的速度沿北偏东45°的方向航行，乙船沿正东方向航行，2小时后甲船到达小岛P处，发现乙船恰好位于甲船正南方向的H处，以O为坐标原点，建立如图所示的直角坐标系．
    （1）P点的坐标是
     
    ，乙船的速度是
     
    海里/小时（结果保留根号）；
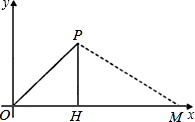    （2）若乙船发现正东方向有另一小岛M，且M位于P点南偏东60°的方向上，若乙船精英家教网速度不变，它再航行多长时间可以到达小岛M？（
    		3
    取1.7，结果保留两个有效数字）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•丹徒区模拟）在一条直线上依次有A、B、C三个港口，甲、乙两船同时分别从A、B港口出发，沿直线匀速驶向C港，最终达到C港．设甲、乙两船行驶x（h）后，与B港的距离分别为y1、y2（km），y1、y2与x的函数关系如图所示．
    （1）填空：A、C两港口间的距离为
    120
    120
    km，a=
    2小时
    2小时
    ；
    （2）求图中点P的坐标，并解释该点坐标所表示的实际意义．

    查看答案和解析>>

    同步练习册答案