
 如图⊙A的圆心在⊙O上,且与⊙O的内接△ABC的边切于点D,⊙A的半径为r,⊙O的半径为R,则此时AB、AC与R、r满足的关系式为:________.
如图⊙A的圆心在⊙O上,且与⊙O的内接△ABC的边切于点D,⊙A的半径为r,⊙O的半径为R,则此时AB、AC与R、r满足的关系式为:________. ∠AOB,可证出△AOE∽△ACD,则
∠AOB,可证出△AOE∽△ACD,则 =
= ,从而得出AB、AC与R、r的关系.
,从而得出AB、AC与R、r的关系.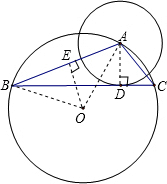 解:如图,
解:如图, =
= ,
,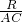 =
=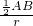 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 (2012•黄埔区一模)如图⊙P的圆心P在⊙O上,⊙O的弦AB所在的直线与⊙P切于C,若⊙P的半径为r,⊙O的半径为R.⊙O和⊙P的面积比为9:4,且PA=10,PB=4.8,DE=5,C、P、D三点共线.
(2012•黄埔区一模)如图⊙P的圆心P在⊙O上,⊙O的弦AB所在的直线与⊙P切于C,若⊙P的半径为r,⊙O的半径为R.⊙O和⊙P的面积比为9:4,且PA=10,PB=4.8,DE=5,C、P、D三点共线.查看答案和解析>>
科目:初中数学 来源:标准大考卷·初中数学AB卷 九年级(上册) (课标华东师大版) (第3版) 课标华东师大版 第3版 题型:022
已知:如图,![]() 的圆心在x轴上,
的圆心在x轴上,![]() 与y轴交于A、B两点.若A点坐标为(0,
与y轴交于A、B两点.若A点坐标为(0,![]() ),则B点的坐标为________.
),则B点的坐标为________.
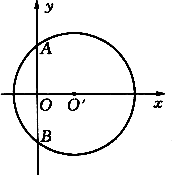
查看答案和解析>>
科目:初中数学 来源:2012届广东省广州黄浦区中考一模数学卷(带解析) 题型:解答题
如图⊙P的圆心P在⊙O上,⊙O的弦AB所在的直线与⊙P切于C,若⊙P的半径为r,⊙O的半径为R.⊙O和⊙P的面积比为9∶4,且PA=10,PB=4.8,DE=5,C、P、D三点共线
(1)求证: ;
;
(2),求AE的长;
(3)连结PD,求sin∠PDA的值.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年广东省广州黄浦区中考一模数学卷(解析版) 题型:解答题
如图⊙P的圆心P在⊙O上,⊙O的弦AB所在的直线与⊙P切于C,若⊙P的半径为r,⊙O的半径为R. ⊙O和⊙P的面积比为9∶4,且PA=10,PB=4.8,DE=5,C、P、D三点共线

(1)求证: ;
;
(2),求AE的长;
(3)连结PD,求sin∠PDA的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com