
 与x轴交于A、C两点,与y轴交于B点.
与x轴交于A、C两点,与y轴交于B点.
 =
= .即∴t=
.即∴t= .
.  =
=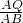 .∴t=
.∴t= >8(舍去)
>8(舍去) 时,以A、P、Q为顶点的三角形与△OAB相似.
时,以A、P、Q为顶点的三角形与△OAB相似. x2-x-8).
x2-x-8). x2-x-8)=8,即x2-6x+12=0,
x2-x-8)=8,即x2-6x+12=0, x2-x-8),四边形OMNB为平行四边形,则MN=OB=8,再根据△<0即可得出结论.
x2-x-8),四边形OMNB为平行四边形,则MN=OB=8,再根据△<0即可得出结论.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案科目:初中数学 来源: 题型:
 如图,抛物线y1与y2都与x轴交于点O(0,0)和点A,y1的顶点是B(2,-1),y2的顶点是C(2,-3),P是y1上的一个动点,过P作y轴的平行线交y2于点Q,分别过P,Q作x轴的平行线,分别交y1,y2于点P′,Q′,连接P′Q′.
如图,抛物线y1与y2都与x轴交于点O(0,0)和点A,y1的顶点是B(2,-1),y2的顶点是C(2,-3),P是y1上的一个动点,过P作y轴的平行线交y2于点Q,分别过P,Q作x轴的平行线,分别交y1,y2于点P′,Q′,连接P′Q′.查看答案和解析>>
科目:初中数学 来源: 题型:
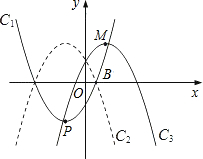 的左侧),点B的横坐标是1;
的左侧),点B的横坐标是1;查看答案和解析>>
科目:初中数学 来源:北京期末题 题型:解答题
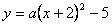 的顶点为P,与x轴相交于A、B两点(点A在点B的左侧),点B的横坐标是1。
的顶点为P,与x轴相交于A、B两点(点A在点B的左侧),点B的横坐标是1。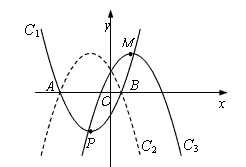
查看答案和解析>>
科目:初中数学 来源: 题型:
 与x轴交于A、B(A在B左侧),顶点为C(1,-2),
与x轴交于A、B(A在B左侧),顶点为C(1,-2),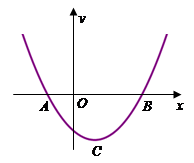
查看答案和解析>>
科目:初中数学 来源:2013年福建省泉州市中考数学模拟试卷(二)(解析版) 题型:解答题
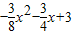 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.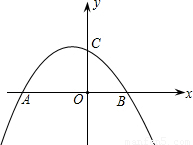
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com